Question

20．如图①，把一张长方形纸板摆放在坐标系中，已知AB=8，AC=17．
（1）求点D坐标．
（2）折三角形纸板ADC，使边CD落在边AC上，设折痕交AD边于点E（图②），求点E坐标．
（3）将三角形纸板ADC沿AC边翻折，翻折后记为△AMC，设AM与BC交于点N，请在图③中画出图形，并求出点N坐标．

Answer 1

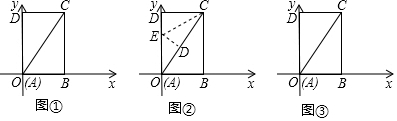
分析 （1）利用勾股定理计算出OD，从而得到D点坐标；
（2）设OE=t，则DE=15-t，由折叠的性质可计算出OD=9，则利用勾股定理得到9²+（15-t）²=t²，然后解方程求出t即可得到E点坐标；
（3）如图③，过点D关于AC的对称点M即可得到△AMC，先利用折叠性质得CD=CN，∠AMC=∠ADC=90°，再证明AN=CN，设BN=m，则CN=AN=15-m，利用勾股定理得到8²+m²=（15-m）²，然后解方程求出m即可得到N点坐标．

解答 解：（1）在RtADC中，∵AD=$\sqrt{1{7}^{2}-{8}^{2}}$=15，
∴D（0，15）；
（2）设OE=t，则DE=15-t，
∵折三角形纸板ADC，使边CD落在边AC上，如图②，
∴OD=17-8=9，
在RtOED中，9²+（15-t）²=t²，解得t=$\frac{51}{5}$，
∴E（0，$\frac{51}{5}$）；
（3）如图③，△AMC为所作，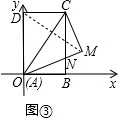

∵三角形纸板ADC沿AC边翻折，翻折后记为△AMC，
∴CD=CN，∠AMC=∠ADC=90°，
在△ABN和△CMN中
$\left\{\begin{array}{l}{∠ANB=∠CNM}\\{∠ABN=∠CMN}\\{AB=CM}\end{array}\right.$，
∴△ABN≌△CMN，
∴AN=CN，
设BN=m，则CN=AN=15-m，
在Rt△ABN中，8²+m²=（15-m）²，解得m=$\frac{161}{30}$，
∴N（8，$\frac{161}{30}$）．

点评 本题考查了作图-对称轴变换：在画一个图形的轴对称图形时，也是先从确定一些特殊的对称点开始的，一般的方法是：由已知点出发向所给直线作垂线，并确定垂足；直线的另一侧，以垂足为一端点，作一条线段使之等于已知点和垂足之间的线段的长，得到线段的另一端点，即为对称点；连接这些对称点，就得到原图形的轴对称图形．也考查了对称轴的性质和勾股定理．