题目内容
12.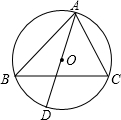 如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC=∠CAD,则弦AC的长为3$\sqrt{2}$cm.
如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC=∠CAD,则弦AC的长为3$\sqrt{2}$cm.
分析 连接CD,根据∠ABC=∠CAD,可得出AC=CD,根据直径所对的圆周角等于90°,以及勾股定理即可得出AC的长.
解答  解:连接CD,
解:连接CD,
∵∠ABC=∠CAD,
∴AC=CD,
∵AD是⊙O的直径,
∴∠ACD=90°,
∵AD=6cm,
∴AC2+CD2=36,
∴AC=3$\sqrt{2}$,
故答案为3$\sqrt{2}$cm.
点评 本题考查了圆周角定理以及等腰直角三角形的性质,根据圆周角相等得出弦相等是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
17.直线y=2x-1一定经过点( )
| A. | (1,0) | B. | (1,2) | C. | (0,2) | D. | (0,-1) |
4.下列结论中,正确的是( )
| A. | 若a>b,则$\frac{1}{a}$<$\frac{1}{b}$ | B. | 若a>b,则a2>b2 | C. | 若a>b,则1-a<1-b | D. | 若a>b,ac2>bc2 |
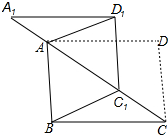 如图,将?ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,分别连结AD、BC.
如图,将?ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,分别连结AD、BC.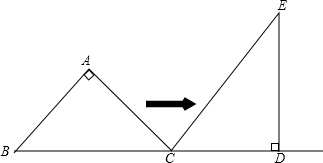 等腰直角三角形△ABC的斜边BC与直角△CDE的直角边CD在同一直线上,∠A=∠EDC=90°,BC=DE=4,CE=5,将△ABC沿着BD向右平移,当点A落在CE上时,平移距离为$\frac{7}{2}$.
等腰直角三角形△ABC的斜边BC与直角△CDE的直角边CD在同一直线上,∠A=∠EDC=90°,BC=DE=4,CE=5,将△ABC沿着BD向右平移,当点A落在CE上时,平移距离为$\frac{7}{2}$.