题目内容
20.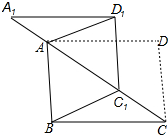 如图,将?ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,分别连结AD、BC.
如图,将?ABCD沿对角线AC剪开,再把△ACD沿CA方向平移得到△A1C1D1,分别连结AD、BC.(1)从线段CA1上找出两对相等的线段;
(2)求证:△A1AD1≌△CC1B.
分析 (1)利用平移的性质得出相等线段即可;
(2)利用平移的性质以及平行线的性质和全等三角形的判定方法SAS得出即可.
解答 (1)解:相等的线段有:AA1=CC1,A1C1=AC
(2)证明:由题意可得:A1D1∥BC,
则∠D1A1A=∠BCC1,
在△A1AD1和△CC1B中
∵$\left\{\begin{array}{l}{A{A}_{1}=C{C}_{1}}\\{∠{D}_{1}{A}_{1}A=∠BC{C}_{1}}\\{{A}_{1}{D}_{1}=C{C}_{1}}\end{array}\right.$,
∴△A1AD1≌△CC1B(SAS).
点评 此题主要考查了平行四边形的性质以及全等三角形的判定与性质等知识,熟练利用平移的性质得出相等的线段是解题关键.

练习册系列答案
相关题目
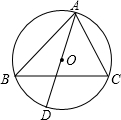 如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC=∠CAD,则弦AC的长为3$\sqrt{2}$cm.
如图,A、B、C、D四点都在⊙O上,AD是⊙O的直径,且AD=6cm,若∠ABC=∠CAD,则弦AC的长为3$\sqrt{2}$cm. 如图,△ABC三边上的半圆面积从小到大依次记为S1,S2,S3,若S1+S2=S3,求证:△ABC是直角三角形.
如图,△ABC三边上的半圆面积从小到大依次记为S1,S2,S3,若S1+S2=S3,求证:△ABC是直角三角形.