题目内容
17.(1)计算:(π-1)0+|2-$\sqrt{2}$|-($\frac{1}{2}$)-1+$\sqrt{8}$+2tan60°-|$\sqrt{3}$-2|-$\sqrt{27}$.(2)解不等式组:$\left\{{\begin{array}{l}{x-3<1}\\{4x-4≥x+2}\end{array}}\right.$.
分析 (1)原式第一项利用零指数幂法则计算,第二项利用绝对值的代数意义化简,第三项利用负指数幂法则计算,第四项化为最简二次根式,第五项利用特殊角的三角函数值计算,第六项利用绝对值的代数意义化简,最后一项化为最简二次根式,计算即可得到结果;
(2)分别求出不等式组中两不等式的解集,找出解集的公共部分即可.
解答 解:(1)原式=1+2-$\sqrt{2}$-2+2$\sqrt{2}$+2×$\sqrt{3}$-2+$\sqrt{3}$-3$\sqrt{3}$=$\sqrt{2}$-1;
(2)$\left\{\begin{array}{l}{x-3<1①}\\{4x-4≥x+2②}\end{array}\right.$,
由①得:x<4;
由②得:x≥2,
则不等式组的解集为2≤x<4.
点评 此题考查了实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
5.下列命题中真命题是( )
| A. | 对角线互相垂直的四边形是矩形 | B. | 对角线相等的四边形是矩形 | ||
| C. | 四条边都相等的四边形是矩形 | D. | 四个内角都相等的四边形是矩形 |
12.南海是我国的固有领土,2014年在我国南海某海域探明可燃冰储量约有194亿立方米.194亿用科学记数法表示为( )
| A. | 1.94×109 | B. | 0.194×1010 | C. | 19.4×109 | D. | 1.94×1010 |
6.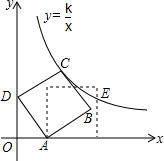 如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,顶点A(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是( )
如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,顶点A(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是( )
 如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,顶点A(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是( )
如图,在平面直角坐标系中,边长为2的正方形ABCD斜靠在y轴上,顶点A(1,0),反比例函数y=$\frac{k}{x}$图象经过点C,将正方形ABCD绕点A顺时针旋转一定角度后,使得点B恰好落在x轴的正半轴上,此时边BC交反比例图象于点E,则点E的纵坐标是( )| A. | $\sqrt{3}$ | B. | $\frac{1}{3}\sqrt{3}+1$ | C. | $\frac{1}{2}\sqrt{3}+1$ | D. | $\frac{3}{2}$ |
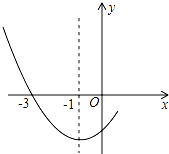 如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),($\frac{5}{2}$,y2)是抛物线上两点,则y1>y2.其中说法正确的有( )个.
如图是二次函数y=ax2+bx+c图象的一部分,其对称轴为x=-1,且过点(-3,0).下列说法:①abc<0;②2a-b=0;③4a+2b+c<0;④若(-5,y1),($\frac{5}{2}$,y2)是抛物线上两点,则y1>y2.其中说法正确的有( )个.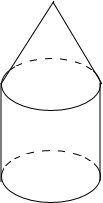 如图,用铁片做成一个上部为圆锥,下部为圆柱的无底活动房外壳,如果圆锥、圆柱的高分别为2米和3米,底面直径为4米,估计一下,做成这个活动房外壳至少需要多少铁皮?
如图,用铁片做成一个上部为圆锥,下部为圆柱的无底活动房外壳,如果圆锥、圆柱的高分别为2米和3米,底面直径为4米,估计一下,做成这个活动房外壳至少需要多少铁皮?