题目内容
如图,在△ABC中,D、E分别是AC、AB边上的点,∠AED=∠C,AB=6,AD=4,AC=5,则AE= .


考点: 相似三角形的判定与性质.
分析: 由在△AED和△ACB中,∠A=∠A,∠AED=∠C,即可证得△AED∽△ACB,然后由相似三角形的对应边成比例,求得AE的长.
解答: 解:在△AED和△ACB中,
∵∠A=∠A,∠AED=∠C,
∴△AED∽△ACB.
∴ ,
,
∴ ,
,
∴AE= .
.
故答案为: .
.
点评: 此题考查了相似三角形的判定与性质.注意△AED与△ACB相似的判定是关键.

练习册系列答案
相关题目
 的图象上,则该函数的图象位于第 象限.
的图象上,则该函数的图象位于第 象限.
 有意义.
有意义.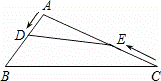
 ,则该正六边形的边长是( )
,则该正六边形的边长是( )