题目内容
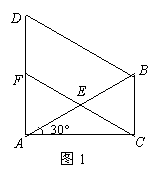
图1,在△ABC中,∠ACB=90°,∠CAB=30°, △ABD是等边三角形,E是AB的中点,连结CE并延长交AD于F.
( 1)求证:① △AEF≌△BEC;② 四边形BCFD是平行四边形;
1)求证:① △AEF≌△BEC;② 四边形BCFD是平行四边形;
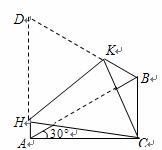
(2)如图2,将四边形ACBD折叠,使D与C重合,HK为折痕,求sin∠ACH的值.
(1)求证:① △AEF≌△BEC;
∠ABC=90°,E是AB的中点,AE=BE,∠FAB=∠EBC=60°,∠FEB=∠BEC
所以△AEF≌△BEC; (3)
② 四边形BCFD是平行四边形;
可得DF∥BC,FC∥DB,或DF∥BC,且DF=BC均可 (3)
(2)设BC=1,则AC= ,AD=AB=2
,AD=AB=2
设DH=x,由折叠得DH=CH=x,(2-x) +3=x
+3=x
X= 所以Sin∠ACH=
所以Sin∠ACH= ( 4 )
( 4 )

练习册系列答案
相关题目

 ,
, ,
, )的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为
)的生长情况进行观察记录.这三个微生物第一天各自一分为二,产生新的微生物(分别被标号为 ,
, ,
, ,
, ,
, ,
, ),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为
),接下去每天都按照这样的规律变化,即每个微生物一分为二,形成新的微生物(课题组成员用如图所示的图形进行形象的记录).那么标号为 的微生物会出现在( )
的微生物会出现在( )
 +(-1)
+(-1) +
+ ×
× -
- -7
-7




 ,则这个等腰三角形的顶角的度数为( )
,则这个等腰三角形的顶角的度数为( ) C.
C. 或
或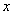 的函数
的函数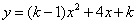 的图像与坐标轴只有2个交点,求
的图像与坐标轴只有2个交点,求 的值.
的值.