题目内容
10.下列式中,运算正确的是:①(22a)2=4a2,②(-$\frac{1}{3}$x+1)(1+$\frac{1}{3}$x)=1-$\frac{1}{9}$x2,③(m-1)2(1-m)3=(m-1)5,④2a×4b×8=2a+2b+3.
| A. | ①② | B. | ②③ | C. | ②④ | D. | ③④ |
分析 根据积的乘方,平方差公式,同底数幂的乘法,幂的乘方分别求出每个式子的值,再逐个判断即可.
解答 解:∵(22a)2=16a2,∴①错误;
∵(-$\frac{1}{3}$x+1)(1+$\frac{1}{3}$x)=1-$\frac{1}{9}$x2,∴②正确;
∵(m-1)2(1-m)3=-(m-1)5,∴③错误;
∵2a×4b×8=2a×22b×23=2a+2b+3,∴④正确;
故选C.
点评 本题考查了积的乘方,平方差公式,同底数幂的乘法,幂的乘方的应用,能根据知识点求出每个式子的值是解此题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
20.下列各式中,变形正确的是( )
| A. | $\frac{x}{y}=\frac{x+y}{2y}$ | B. | $\frac{m+b}{a-b}=\frac{m+1}{a-1}$ | C. | $\frac{a}{b}=\frac{a•m}{b•m}$ | D. | $\frac{{x}^{2}-{y}^{2}}{y+x}=x-y$ |
 有理数a、b在数轴上的位置如图所示.化简:|2-3b|-2|2+b|+|a-2|-|3b-2a|.
有理数a、b在数轴上的位置如图所示.化简:|2-3b|-2|2+b|+|a-2|-|3b-2a|.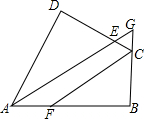 如图,四边形ABCD中,AE平分∠DAB,CF平分∠DCB,且AE∥CF.
如图,四边形ABCD中,AE平分∠DAB,CF平分∠DCB,且AE∥CF.