题目内容
2．正方形具备而矩形不具备的特征是（ ）| A． | 对角线互相垂直 | B． | 对角线相等 | ||
| C． | 对角线互相平分且相等 | D． | 对角线互相平分 |
分析 对正方形的性质和矩形的性质进行对比，从而得到答案．
解答 解：正文形的性质有：①正方形的四条边都相等，四个角都是直角；
②正方形的两条对角线相等，互相垂直平分，并且每条对角线平分一组对角；
③正方形具有四边形、平行四边形、矩形、菱形的一切性质．
矩形的性质有：①平行四边形的性质矩形都具有；
②矩形的四个角都是直角；
③矩形的对角线相等；
④矩形是轴对称图形，它有2条对称轴
经过对比可得出，正方形具有但矩形不具有的性质有：对角线互相垂直．
故选A．
点评 本题主要考查了正方形和矩形的性质，解题的关键是掌握正方形和矩形的各种性质，此题难度不大．
练习册系列答案
阅读快车系列答案
相关题目
10．已知⊙O的半径为1，弦AB长为1，则弦AB所对的圆周角为（ ）
| A． | 60° | B． | 30° | C． | 60°和120° | D． | 30°和150° |
17．下列方程中，是一元二次方程的有（ ）
①x2+3x=$\frac{2}{x}$ ②7x2=0 ③$\frac{1}{5}$x2-$\frac{\sqrt{2}}{2}$=x ④x（1-2x2）=2x2 ⑤2x2-5y=0．
①x2+3x=$\frac{2}{x}$ ②7x2=0 ③$\frac{1}{5}$x2-$\frac{\sqrt{2}}{2}$=x ④x（1-2x2）=2x2 ⑤2x2-5y=0．
| A． | 1个 | B． | 2个 | C． | 3个 | D． | 4个 |
11．
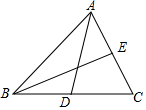如图，AD和BE是△ABC的两条中线，设△ABD的面积为S1，△BCE的面积为S2，那么（ ）
如图，AD和BE是△ABC的两条中线，设△ABD的面积为S1，△BCE的面积为S2，那么（ ）| A． | S1＞S2 | B． | S1=S2 | C． | S1＜S2 | D． | 不能确定 |
12．下列方程是二元一次方程的是（ ）
| A． | xy+3x=7 | B． | $\frac{1}{x}+y=5$ | C． | 2x-y=2 | D． | x2+y=1 |