题目内容
2.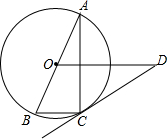 已知:如图,AB是⊙O的直径,BC是⊙O的弦,点D是⊙O外一点,∠DCA=∠B.
已知:如图,AB是⊙O的直径,BC是⊙O的弦,点D是⊙O外一点,∠DCA=∠B.(1)求证:DC是⊙O的切线;
(2)若OD∥BC,且OD=5,BC=2.求⊙O的半径.
分析 (1)连结OC,如图,根据圆周角定理得到∠ACB=90°,即∠OCB+∠OCA=90°,加上∠B=∠OCB,∠DCA=∠B,则∠OCA+∠DCA=90°,即∠OCD=90°,于是根据切线的判定定理即可得到DC是⊙O的切线;
(2)设⊙O的半径为r,根据平行线的性质,由OD∥BC得到∠COD=∠OCB,而∠B=∠OCB,所以∠B=∠COD,于是根据相似三角形的判定方法得到Rt△ABC∽Rt△DOC,然后利用相似的性质得$\frac{2}{r}$=$\frac{2r}{5}$,再根据比例性质求出r即可.
解答  (1)证明:连结OC,如图,
(1)证明:连结OC,如图,
∵AB是⊙O的直径,
∴∠ACB=90°,即∠OCB+∠OCA=90°,
∵OB=OC,
∴∠B=∠OCB,
而∠DCA=∠B,
∴∠OCB=∠DCA,
∴∠OCA+∠DCA=90°,即∠OCD=90°,
∴OC⊥CD,
∴DC是⊙O的切线;
(2)解:设⊙O的半径为r,
∵OD∥BC,
∴∠COD=∠OCB,
而∠B=∠OCB,
∴∠B=∠COD,
∴Rt△ABC∽Rt△DOC,
∴$\frac{BC}{OC}$=$\frac{AB}{OD}$,即$\frac{2}{r}$=$\frac{2r}{5}$,解得r=$\sqrt{5}$,
即⊙O的半径为$\sqrt{5}$.
点评 本题考查了切线的判定:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了相似三角形的判定与性质.

练习册系列答案
相关题目
1. 下列四个物体的俯视图与给出视图一致的是( )
下列四个物体的俯视图与给出视图一致的是( )
 下列四个物体的俯视图与给出视图一致的是( )
下列四个物体的俯视图与给出视图一致的是( )| A. | 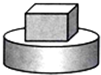 | B. | 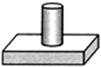 | C. | 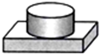 | D. |  |
10.高速公路上,从3千米处开始,每隔4千米经过一个限速标志牌,并且从10千米处开始,每隔9千米经过一个速度监控仪,司机小王刚好在19千米的A处第一次同时经过这两种设施,那么,司机小王第二次同时经过这两种设施需要从A处继续行驶( )千米.
| A. | 36 | B. | 37 | C. | 55 | D. | 91 |
17.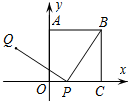 如图,正方形OABC的一个顶点O是平面直角坐标系的原点,顶点A,C分别在y轴和x轴上,P为边OC上的一个动点,且PQ⊥BP,PQ=BP,当点P从点C运动到点O时,可知点Q始终在某函数图象上运动,则其函数图象是( )
如图,正方形OABC的一个顶点O是平面直角坐标系的原点,顶点A,C分别在y轴和x轴上,P为边OC上的一个动点,且PQ⊥BP,PQ=BP,当点P从点C运动到点O时,可知点Q始终在某函数图象上运动,则其函数图象是( )
 如图,正方形OABC的一个顶点O是平面直角坐标系的原点,顶点A,C分别在y轴和x轴上,P为边OC上的一个动点,且PQ⊥BP,PQ=BP,当点P从点C运动到点O时,可知点Q始终在某函数图象上运动,则其函数图象是( )
如图,正方形OABC的一个顶点O是平面直角坐标系的原点,顶点A,C分别在y轴和x轴上,P为边OC上的一个动点,且PQ⊥BP,PQ=BP,当点P从点C运动到点O时,可知点Q始终在某函数图象上运动,则其函数图象是( )| A. | 线段 | B. | 圆弧 | C. | 双曲线的一部分 | D. | 抛物线的一部分 |
12.已知关于x的方程(1-2k)x2-2$\sqrt{k+1}$x-1=0有实数根,则k的取值范围是( )
| A. | k≥2 | B. | k≤2 | C. | -1≤k≤2 | D. | -1≤k≤2且$k≠\frac{1}{2}$ |