题目内容
若b,c满足(2c+b-12)2+
=0,又知a=6,则以a,b,c为边长组成的三角形的面积等于 .
2tan45°-
|
考点:勾股定理,非负数的性质:偶次方,非负数的性质:算术平方根,等腰三角形的性质,特殊角的三角函数值
专题:
分析:先根据非负数的性质及特殊角的三角函数值求出c,b的值,再过A作AD⊥BC于D,根据等腰三角形的性质得出BD=DC=
BC=3.在直角△ABD中,由勾股定理,得出AD=
=
,然后根据△ABC的面积=
BC•AD即可求解.
| 1 |
| 2 |
| AB2-BD2 |
| 7 |
| 1 |
| 2 |
解答: 解:∵(2c+b-12)2+
解:∵(2c+b-12)2+
=0,
∴2c+b-12=0,2tan45°-
b=0,
∴b=4,c=4.
如图,△ABC中,AB=AC=4,BC=6.
过A作AD⊥BC于D,则BD=DC=
BC=3.
在直角△ABD中,由勾股定理,得
AD=
=
=
,
∴△ABC的面积=
BC•AD=
×6×
=3
.
故答案为3
.
 解:∵(2c+b-12)2+
解:∵(2c+b-12)2+2tan45°-
|
∴2c+b-12=0,2tan45°-
| 1 |
| 2 |
∴b=4,c=4.
如图,△ABC中,AB=AC=4,BC=6.
过A作AD⊥BC于D,则BD=DC=
| 1 |
| 2 |
在直角△ABD中,由勾股定理,得
AD=
| AB2-BD2 |
| 42-32 |
| 7 |
∴△ABC的面积=
| 1 |
| 2 |
| 1 |
| 2 |
| 7 |
| 7 |
故答案为3
| 7 |
点评:本题考查了特殊角的三角函数值,非负数的性质,勾股定理,三角形的面积,准确作出辅助线是解题的关键.

练习册系列答案
相关题目
 如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AE的长为
如图,点A,B,C,D为⊙O上的四个点,AC平分∠BAD,AC交BD于点E,CE=4,CD=6,则AE的长为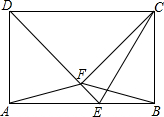 如图,E为矩形ABCD边AB上一点,AB=14,CE=13,DE=15,CF⊥DE于点F,连结AF、BF.则△ABF的面积为
如图,E为矩形ABCD边AB上一点,AB=14,CE=13,DE=15,CF⊥DE于点F,连结AF、BF.则△ABF的面积为