题目内容
20. 如图所示,已知直线y=x+3的图象与 x轴、y轴交于A,B两点,直线l经过原点,与线段AB交于点C,把△AOB的面积分为2:1的两部分,求直线l的解析式.
如图所示,已知直线y=x+3的图象与 x轴、y轴交于A,B两点,直线l经过原点,与线段AB交于点C,把△AOB的面积分为2:1的两部分,求直线l的解析式.
分析 根据直线y=x+4的解析式可求出A、B两点的坐标,如图:
(1)当直线l把△ABO的面积分为S△AOC:S△BOC=2:1时,作CF⊥OA于F,CE⊥OB于E,可分别求出△AOB与△AOC的面积,再根据其面积公式可求出两直线交点的坐标,从而求出其解析式;
(2)当直线l把△ABO的面积分为S△AOC:S△BOC=1:2时,同(1).
解答 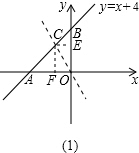 解:由直线y=x+4的解析式可求得A(-3,O)、B(0,3),
解:由直线y=x+4的解析式可求得A(-3,O)、B(0,3),
如图(1),当直线l把△AOB的面积分为S△AOC:S△BOC=2:1时,
作CF⊥OA于F,CE⊥OB于E,则S△AOB=$\frac{9}{2}$,则S△AOC=3,
∴$\frac{1}{2}$AO•CF=3,即$\frac{1}{2}$×3×CF=3,
∴CF=2.
同理,解得CE=1.
∴C(-1,2),
∴直线l的解析式为y=-2x;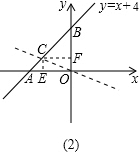
如图(2),当直线l把△ABO的面积分为S△AOC:S△BOC=1:2时,
同理求得C(-2,1),
∴直线l的解析式为y=-$\frac{1}{2}$x.
故答案为y=-2x或y=-$\frac{1}{2}$x.
点评 此题考查的是两直线相交和平行问题,用待定系数法求一次函数的解析式,涉及到三角形的面积公式及分类讨论的方法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.请思考下列命题的逆命题:①对顶角相等;②角平分线上的点到角两边的距离相等;③到线段两个端点距离相等的点在这条线段的垂直平分线上;④两个全等直角三角形的面积相等,其中逆命题不正确的命题的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
9. 为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分:
为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分:
根据以上信息,解答下列问题:
(1)该调查方式是抽样调查;(填“普查”或者“抽样调查”)
(2)本次调查的家庭数为50户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是18%.
(3)若该小区共有1000户家庭,请估计该月用水量不超过9.0吨的家庭数.
 为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分:
为了解某小区某月家庭用水量的情况,从该小区随机抽取部分家庭进行调查,以下是根据调查数据绘制的统计图表的一部分:| 分组 | 家庭用水量x/吨 | 家庭数/户 |
| A | 0≤x≤4.0 | 4 |
| B | 4.0<x≤6.5 | 13 |
| C | 6.5<x≤9.0 | |
| D | 9.0<x≤11.5 | |
| E | 11.5<x≤14.0 | 6 |
| F | x>14.0 | 3 |
(1)该调查方式是抽样调查;(填“普查”或者“抽样调查”)
(2)本次调查的家庭数为50户,家庭用水量在9.0<x≤11.5范围内的家庭数占被调查家庭数的百分比是18%.
(3)若该小区共有1000户家庭,请估计该月用水量不超过9.0吨的家庭数.
