题目内容
【题目】(2016吉林省)如图,在等腰直角三角形ABC中,∠BAC=90°,AC=![]() cm,AD⊥BC于点D,点P从点A出发,沿A→C方向以
cm,AD⊥BC于点D,点P从点A出发,沿A→C方向以![]() cm/s的速度运动到点C停止,在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
cm/s的速度运动到点C停止,在运动过程中,过点P作PQ∥AB交BC于点Q,以线段PQ为边作等腰直角三角形PQM,且∠PQM=90°(点M,C位于PQ异侧).设点P的运动时间为x(s),△PQM与△ADC重叠部分的面积为y(cm2)
(1)当点M落在AB上时,x= ;
(2)当点M落在AD上时,x= ;
(3)求y关于x的函数解析式,并写出自变量x的取值范围.
【答案】(1)4;(2)![]() ;(3)
;(3)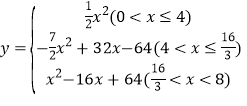 .
.
【解析】试题分析:(1)当点M落在AB上时,四边形AMQP是正方形,此时点D与点Q重合,由此即可解决问题.
(2)如图1中,当点M落在AD上时,作PE⊥QC于E,先证明DQ=QE=EC,由PE∥AD,得![]() =
=![]() ,由此即可解决问题.
,由此即可解决问题.
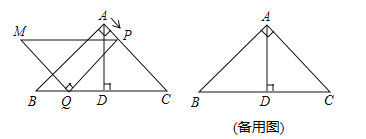
(3)分三种情形①当0<x≤4时,如图2中,设PM、PQ分别交AD于点E、F,则重叠部分为△PEF,②当4<x≤![]() 时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.③当
时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.③当![]() <x<8时,如图4中,则重合部分为△PMQ,分别计算即可解决问题.
<x<8时,如图4中,则重合部分为△PMQ,分别计算即可解决问题.
试题解析:解:(1)当点M落在AB上时,四边形AMQP是正方形,此时点D与点Q重合,AP=CP=![]() ,所以x=
,所以x=![]() =4.故答案为:4.
=4.故答案为:4.
(2)如图1中,当点M落在AD上时,作PE⊥QC于E.

∵△MQP,△PQE,△PEC都是等腰直角三角形,MQ=PQ=PC,∴DQ=QE=EC,∵PE∥AD,∴![]() =
=![]() ,∵AC=
,∵AC=![]() ,∴PA=
,∴PA=![]() ,∴x=
,∴x=![]() ÷
÷![]() =
=![]() .故答案为:
.故答案为:![]() .
.
(3)①当0<x≤4时,如图2中,设PM、PQ分别交AD于点E、F,则重叠部分为△PEF,
∵AP=![]() x,∴EF=PE=x,∴y=S△PEF=
x,∴EF=PE=x,∴y=S△PEF=![]() PEEF=
PEEF=![]() .
.
②当4<x≤![]() 时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.
时,如图3中,设PM、MQ分别交AD于E、G,则重叠部分为四边形PEGQ.

∵PQ=PC=![]() ,∴PM=16﹣2x,∴ME=PM﹣PE=16﹣3x,∴y=S△PMQ﹣S△MEG=
,∴PM=16﹣2x,∴ME=PM﹣PE=16﹣3x,∴y=S△PMQ﹣S△MEG=![]() =
=![]() .
.

③当![]() <x<8时,如图4中,则重合部分为△PMQ,∴y=S△PMQ=
<x<8时,如图4中,则重合部分为△PMQ,∴y=S△PMQ=![]() =
=![]() =
=![]() .
.
综上所述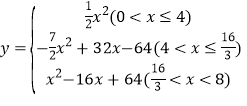 .
.

 学练快车道快乐假期暑假作业新疆人民出版社系列答案
学练快车道快乐假期暑假作业新疆人民出版社系列答案 浙大优学小学年级衔接导与练浙江大学出版社系列答案
浙大优学小学年级衔接导与练浙江大学出版社系列答案 小学暑假作业东南大学出版社系列答案
小学暑假作业东南大学出版社系列答案 津桥教育暑假拔高衔接广东人民出版社系列答案
津桥教育暑假拔高衔接广东人民出版社系列答案 波波熊暑假作业江西人民出版社系列答案
波波熊暑假作业江西人民出版社系列答案