题目内容
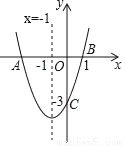
如图,二次函数y=ax2+bx+c(a≠0)的图象与x轴交于点A、B两点,与y轴交于点C,对称轴为直线x=﹣1,点B的坐标为(1,0),则下列结论:①AB=4;②b2﹣4ac>0;③ab<0;④a2﹣ab+ac<0,其中正确的结论有( )个.
A. 1个 B. 2个 C. 3个 D. 4个
C 【解析】试题解析:∵抛物线的对称轴为直线x=-1,点B的坐标为(1,0), ∴A(-3,0), ∴AB=1-(-3)=4,所以①正确; ∵抛物线与x轴有2个交点, ∴△=b2-4ac>0,所以②正确; ∵抛物线开口向下, ∴a>0, ∵抛物线的对称轴为直线x=-=-1, ∴b=2a>0, ∴ab>0,所以③错误; ∵x=-1时,...
练习册系列答案
相关题目


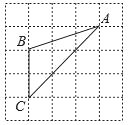
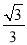 B.
B. 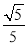 C.
C. 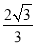 D.
D. 
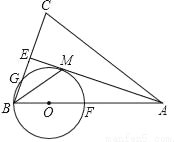
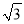 的坡面向下走了20米的路,那么他竖直方向下降的高度为_____.
的坡面向下走了20米的路,那么他竖直方向下降的高度为_____.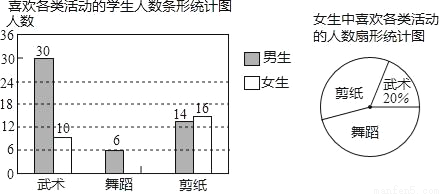
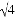 ,
,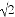 ,3.14,
,3.14, 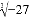 ,
, ,这6个数中,无理数共有( )
,这6个数中,无理数共有( )