题目内容
 有一座桥的桥洞是120°的弧形,它的跨度AB为
有一座桥的桥洞是120°的弧形,它的跨度AB为 米,有一只大船装满货物后船宽10米,高4米,问该船能否经过,并通过计算说明理由.
米,有一只大船装满货物后船宽10米,高4米,问该船能否经过,并通过计算说明理由.
 解:连接OA、OD、OM,设OA=r,
解:连接OA、OD、OM,设OA=r,∵
 =120°,
=120°,∴∠AOD=60°,
∴OD=
 ,
,∵AB⊥CD,AB=10
 m,
m,∴AD=
 =5
=5 m,
m,在Rt△AOD中,
OD2+AD2=OA2,即(
 )2+(5
)2+(5 )2=r2,解得r=10m,
)2=r2,解得r=10m,在Rt△MDH中,
∵MN⊥CD,
∴MH=
 =
=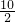 =5m,
=5m,∴HO=
 =
=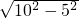 =5
=5 m,
m,∴DH=HO-OD=5
 -5≈3.65m<4m,故该船不能通过.
-5≈3.65m<4m,故该船不能通过.分析:先连接OA、OD、OM,设OA=r,由
 =120°可知∠AOD=60°,则OD=
=120°可知∠AOD=60°,则OD= ,由垂径定理可知AD=
,由垂径定理可知AD= =5
=5 ,在Rt△AOD中利用勾股定理求出R的值,再在Rt△MOH中利用勾股定理求出HD的值与4米相比较即可得出结论.
,在Rt△AOD中利用勾股定理求出R的值,再在Rt△MOH中利用勾股定理求出HD的值与4米相比较即可得出结论.点评:本题考查的是垂径定理的应用及勾股定理,解答此题的关键是根据题意作出辅助线,构造出直角三角形,再利用勾股定理解答.

练习册系列答案
相关题目
 如图,有一座石拱桥的桥拱是以O为圆心,OA为半径的一段圆弧.若∠AOB=120°,OA=4米,请求出石拱桥的高度.
如图,有一座石拱桥的桥拱是以O为圆心,OA为半径的一段圆弧.若∠AOB=120°,OA=4米,请求出石拱桥的高度. 有一座桥的桥洞是120°的弧形,它的跨度AB为
有一座桥的桥洞是120°的弧形,它的跨度AB为 米,有一只大船装满货物后船宽10米,高4米,问该船能否经过,并通过计算说明理由.
米,有一只大船装满货物后船宽10米,高4米,问该船能否经过,并通过计算说明理由.
 米,有一只大船装满货物后船宽10米,高4米,问该船能否经过,并通过计算说明理由.
米,有一只大船装满货物后船宽10米,高4米,问该船能否经过,并通过计算说明理由.