题目内容
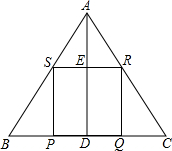 如图,在等腰△ABC中,底边BC=12cm,高AD=8cm,四边形PQRS是正方形.
如图,在等腰△ABC中,底边BC=12cm,高AD=8cm,四边形PQRS是正方形.(1)△ASR与△ABC相似吗?为什么?
(2)求正方形PQRS的边长.
考点:相似三角形的判定与性质,等腰三角形的性质,正方形的性质
专题:
分析:(1)由题意得SR∥BC,故∠ASR=∠B;而∠SAR=∠BAC,即可证明△ASR∽△ABC.
(2)设SR=SP=λ,表示出AE=8-λ;根据△ASR∽△ABC,列出关于λ的比例式,求出λ即可解决问题.
(2)设SR=SP=λ,表示出AE=8-λ;根据△ASR∽△ABC,列出关于λ的比例式,求出λ即可解决问题.
解答: 解:(1)△ASR∽△ABC;理由如下:
解:(1)△ASR∽△ABC;理由如下:
∵四边形PQRS是正方形,
∴SR∥BC,∠ASR=∠B;而∠SAR=∠BAC,
∴△ASR∽△ABC.
(2)∵四边形PQRS是正方形,
∴SR=SP(设为λ),而AD⊥BC,
∴DE=PS=λ,AE=8-λ;
∵△ASR∽△ABC,
∴
=
,即
=
,
解得:λ=
,
即正方形PQRS的边长为
(cm).
 解:(1)△ASR∽△ABC;理由如下:
解:(1)△ASR∽△ABC;理由如下:∵四边形PQRS是正方形,
∴SR∥BC,∠ASR=∠B;而∠SAR=∠BAC,
∴△ASR∽△ABC.
(2)∵四边形PQRS是正方形,
∴SR=SP(设为λ),而AD⊥BC,
∴DE=PS=λ,AE=8-λ;
∵△ASR∽△ABC,
∴
| SR |
| BC |
| AE |
| AD |
| λ |
| 12 |
| 8-λ |
| 8 |
解得:λ=
| 24 |
| 5 |
即正方形PQRS的边长为
| 24 |
| 5 |
点评:该题主要考查了相似三角形的判定及其性质的应用问题;解题的关键是深入把握题意,准确找出图形中的对应元素,正确列出比例式来分析、判断或解答.

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目
 如图,∠AOC,∠BOD都是直角,∠AOB:∠AOD=5:17,求∠AOB与∠COD的度数.
如图,∠AOC,∠BOD都是直角,∠AOB:∠AOD=5:17,求∠AOB与∠COD的度数.
 已知在△ABC中,∠A=90°,AD⊥BC于点D,M为AD中点,BM的延长线交AC于点P,PQ⊥BC于Q.求证:PQ2=PA•PC.
已知在△ABC中,∠A=90°,AD⊥BC于点D,M为AD中点,BM的延长线交AC于点P,PQ⊥BC于Q.求证:PQ2=PA•PC. 如图,已知线段AB=4cm,延长线段AB到C,使BC=2AB.
如图,已知线段AB=4cm,延长线段AB到C,使BC=2AB.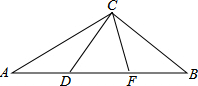 如图所示,△CDF是等边三角形,且∠ACB=120°.
如图所示,△CDF是等边三角形,且∠ACB=120°. 如图,在大小为4×4的正方形方格中,△ABC的顶点A、B、C在单位正方形的顶点上,
如图,在大小为4×4的正方形方格中,△ABC的顶点A、B、C在单位正方形的顶点上,