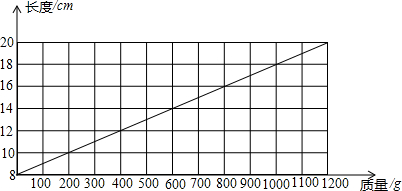
题目内容
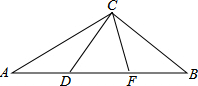 如图所示,△CDF是等边三角形,且∠ACB=120°.
如图所示,△CDF是等边三角形,且∠ACB=120°.(1)找出图中所有的相似三角形;
(2)求证:FD2=AD•BF.
考点:相似三角形的判定与性质
专题:
分析:(1)根据条件可得∠ADC=∠CFB=∠ACB=120°,∠ACD=∠CBF,可得出三角形相似;
(2)根据(1)中的△ACD∽△CBF,结合CF=CD=DF,可证得结论.
(2)根据(1)中的△ACD∽△CBF,结合CF=CD=DF,可证得结论.
解答:(1)解:∵△CDF为等边三角形,
∴∠CDF=∠CFD=∠DCF=60°,
∴∠ADC=∠CFB=∠ACB=120°,
在△ACD和△ABC中又∠CAD=∠BAC,
∴△ACD∽△ABC,
同理△BCF∽△BAC,
又∵∠A+∠ACD=∠CDF=60°,∠ACD+∠BCF=120°-∠DCF=60°,
∴∠A=∠BCF,
∴△ACD∽△CBF;
(2)证明:∵△ACD∽△CBF,
∴
=
,
∴CF•CD=AD•BF,
又∵CF=CD=FD,
∴FD2=AD•BF.
∴∠CDF=∠CFD=∠DCF=60°,
∴∠ADC=∠CFB=∠ACB=120°,
在△ACD和△ABC中又∠CAD=∠BAC,
∴△ACD∽△ABC,
同理△BCF∽△BAC,
又∵∠A+∠ACD=∠CDF=60°,∠ACD+∠BCF=120°-∠DCF=60°,
∴∠A=∠BCF,
∴△ACD∽△CBF;
(2)证明:∵△ACD∽△CBF,
∴
| AD |
| CF |
| CD |
| BF |
∴CF•CD=AD•BF,
又∵CF=CD=FD,
∴FD2=AD•BF.
点评:本题主要考查相似三角形的判定和性质及等边三角形的性质,掌握相似三角形的对应边成比例是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
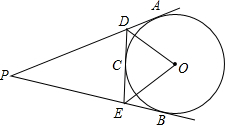 如图,P是圆O外的一点,PA、PB与圆O分别相切于点A、B,C是劣弧
如图,P是圆O外的一点,PA、PB与圆O分别相切于点A、B,C是劣弧 |
| AB |
| A、38° | B、52° |
| C、70° | D、71° |
 如图,B是AC的中点,D是CE中点.试说明:BD=
如图,B是AC的中点,D是CE中点.试说明:BD=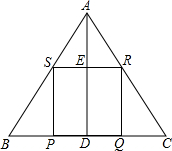 如图,在等腰△ABC中,底边BC=12cm,高AD=8cm,四边形PQRS是正方形.
如图,在等腰△ABC中,底边BC=12cm,高AD=8cm,四边形PQRS是正方形.