题目内容
8. 已知:点A、E、D、C在同一条直线上,AE=CD,EF∥BD,EF=BD.求证:AB∥CF.
已知:点A、E、D、C在同一条直线上,AE=CD,EF∥BD,EF=BD.求证:AB∥CF.
分析 首先利用SAS证明△ABD≌△CEF,根据全等三角形对应角相等,可得∠A=∠C,再根据“内错角相等,两直线平行”,即可证出AB∥CF.
解答 证明:∵AE=CD,
∴AE+ED=CD+ED,
即:AD=CE,
∵EF∥BD,
∴∠BDA=∠CEF,
在△ABD和△CEF中,
$\left\{\begin{array}{l}{AD=CE}\\{∠BDA=∠CEF}\\{EF=BD}\end{array}\right.$,
∴△ABD≌△CEF(SAS),
∴∠A=∠C,
∴AB∥CF.
点评 此题主要考查了平行线的性质,全等三角形的判定,做题的关键是找出证三角形全等的条件.

练习册系列答案
相关题目
3.PM 2.5是指大气中直径小于或等于2.5微米的颗粒物,它能较长时间悬浮于空气中,其在空气中含量浓度越高,就代表空气污染越严重.其中2.5微米=0.0000025米,用科学记数法表示为( )
| A. | 0.25×10-5米 | B. | 2.5×10-5米 | C. | 2.5×10-6米 | D. | 25×10-7米 |
20.关于x的分式方程:$\frac{1-x}{x-2}=\frac{1}{2-x}-a$有增根,则增根可能是( )
| A. | x=1 | B. | x=0 | C. | x=2 | D. | x=a |
 如图,反比例函数$y=\frac{k}{x}(k>0)$的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=3,则k的值为12.
如图,反比例函数$y=\frac{k}{x}(k>0)$的图象与矩形ABCO的两边相交于E,F两点,若E是AB的中点,S△BEF=3,则k的值为12.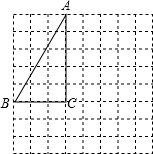 如图,在一个正方形网格中有一个△ABC(定点都在格点上).
如图,在一个正方形网格中有一个△ABC(定点都在格点上). 河的一旁有两个村子A、B,要在河边建一水泵站引水到村里.一村民画了一张图,以直线l表示一条河,求作一点P,使P到A、B的距离和最短,作出P点,并用几何语言叙述你的理由.
河的一旁有两个村子A、B,要在河边建一水泵站引水到村里.一村民画了一张图,以直线l表示一条河,求作一点P,使P到A、B的距离和最短,作出P点,并用几何语言叙述你的理由.