题目内容
 如图,在△ABC中,∠B的平分线与∠C的外角平分线相交于D,DG∥BC交AC,AB于F,G.求证:GF=BG-CF.
如图,在△ABC中,∠B的平分线与∠C的外角平分线相交于D,DG∥BC交AC,AB于F,G.求证:GF=BG-CF.考点:等腰三角形的判定与性质
专题:证明题
分析:先证明∠ABD=∠GDB,∠ACD=∠FDC,得出BG=DG,CF=DF,从而证出GF=BG-CF.
解答:解:∵BD平分∠ABC,CD平分∠ACE,
∴∠ABD=∠CBD,∠ACD=∠ECD,
∵DG∥BC,
∴∠GDB=∠CBD,∠FDC=∠ECD,
∴∠ABD=∠GDB,∠ACD=∠FDC,
∴BG=DG,CF=DF,
∵GF=DG-DF,
∴GF=BG-CF.
∴∠ABD=∠CBD,∠ACD=∠ECD,
∵DG∥BC,
∴∠GDB=∠CBD,∠FDC=∠ECD,
∴∠ABD=∠GDB,∠ACD=∠FDC,
∴BG=DG,CF=DF,
∵GF=DG-DF,
∴GF=BG-CF.
点评:本题考查了平行线的性质、角平分线的定义以及等腰三角形的判定;弄清角之间的相等关系证出相等线段是解题的关键.

练习册系列答案
相关题目
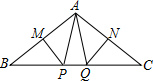 如图,△ABC中,MP和NQ分别垂直平分AB和AC,若∠PAQ=40°,则∠BAC的度数是( )
如图,△ABC中,MP和NQ分别垂直平分AB和AC,若∠PAQ=40°,则∠BAC的度数是( )| A、140° | B、110° |
| C、100° | D、70° |
 如图,点O(0,0),A(2,2),若存在格点P,使△APO为等腰直角三角形,则点P的个数为( )
如图,点O(0,0),A(2,2),若存在格点P,使△APO为等腰直角三角形,则点P的个数为( )| A、4 | B、5 | C、6 | D、8 |
 如图,△ABC的边长不变,BC边上的高AH的长为x在变化,若BC的长为8,则△ABC的面积y与x之间的函数关系式为
如图,△ABC的边长不变,BC边上的高AH的长为x在变化,若BC的长为8,则△ABC的面积y与x之间的函数关系式为 如图所示,甲、乙二人沿着边长为90米的正方形,按A→B→C→D→A…的方向运行,甲从A以72米/分的速度行走,乙从B以57米/分的速度行走.
如图所示,甲、乙二人沿着边长为90米的正方形,按A→B→C→D→A…的方向运行,甲从A以72米/分的速度行走,乙从B以57米/分的速度行走. 如图,矩形ABCD的边AD长为2,AB长为1,点A在数轴上对应的数是-1,以A点为圆心,对角线AC长为半径画弧,交数轴于点E,则这个点E表示的实数是( )
如图,矩形ABCD的边AD长为2,AB长为1,点A在数轴上对应的数是-1,以A点为圆心,对角线AC长为半径画弧,交数轴于点E,则这个点E表示的实数是( ) 如图,C岛在A岛的北偏东55°的方向,B岛在A岛的北偏东75°的方向,C岛在B岛的北偏西35°的方向.∠ACB的平分线CM交AB于点M.
如图,C岛在A岛的北偏东55°的方向,B岛在A岛的北偏东75°的方向,C岛在B岛的北偏西35°的方向.∠ACB的平分线CM交AB于点M.