题目内容
11. 如图,△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB于D,PE⊥AC于E.若AB=6cm,AC=10cm,则AD=2cm.
如图,△ABC的外角∠DAC的平分线交BC边的垂直平分线于P点,PD⊥AB于D,PE⊥AC于E.若AB=6cm,AC=10cm,则AD=2cm.
分析 利用“HL”证明Rt△ADP和Rt△AEP全等,根据全等三角形对应边相等可得AD=AE,再根据AB、AC的长度表示出AD、CE,然后解方程即可.
解答 解:在Rt△ADP和Rt△AEP中,$\left\{\begin{array}{l}{AP=AP}\\{DP=EP}\end{array}\right.$,
∴Rt△ADP≌Rt△AEP(HL),
∴AD=AE,
∵AB=6cm,AC=10cm,
∴6+AD=10-AE,
即6+AD=10-AD,
解得AD=2cm,
故答案为:2
点评 本题考查了全等三角形的判定与性质,利用“HL”证明Rt△ADP和Rt△AEP全等是解题的关键.

练习册系列答案
相关题目
8.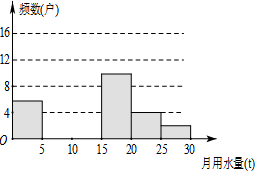 八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
请解答以下问题:
(1)填空:m=12,n=0.08,并把频数分布直方图补充完整;
(2)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?
 八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,
八(1)班同学为了解2015年某小区家庭月均用水情况,随机调查了该小区部分家庭,并将调查数据进行如下整理,| 月均用水量x(t) | 频数(户) | 频率 |
| 0<x≤5 | 6 | 0.12 |
| 5<x≤10 | m | 0.24 |
| 10<x≤15 | 16 | 0.32 |
| 15<x≤20 | 10 | 0.20 |
| 20<x≤25 | 4 | n |
| 60≤x<70 | 2 | 0.04 |
(1)填空:m=12,n=0.08,并把频数分布直方图补充完整;
(2)若该小区有1000户家庭,求该小区月均用水量超过10t的家庭大约有多少户?
6.化简-$\sqrt{-{x}^{3}}$的结果是( )
| A. | x$\sqrt{-x}$ | B. | -x$\sqrt{-x}$ | C. | x$\sqrt{x}$ | D. | -x$\sqrt{x}$ |
1.下列计算正确的是( )
| A. | (m-2n)(m-n)=m2-3mn+2n2 | B. | (m+1)2=m2-1 | ||
| C. | -m(m2-m-1)=-m3+m2-m | D. | (m+n)(m2+mn+n2)=m3+n2 |

 如图,在△ABC中,分别以AB,AC为边向外作等腰直角三角形ABE,等腰直角三角形ACD,其中∠BAE=∠CAD=90°,BD与CE相交于点O,则:∠DOE的大小是否会随着∠BAC大小的变化而变化?如不变,请求出∠DOE的大小?如变化,说明理由.
如图,在△ABC中,分别以AB,AC为边向外作等腰直角三角形ABE,等腰直角三角形ACD,其中∠BAE=∠CAD=90°,BD与CE相交于点O,则:∠DOE的大小是否会随着∠BAC大小的变化而变化?如不变,请求出∠DOE的大小?如变化,说明理由. 如图,抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于点C,且OB=OC=3OA.直线y=-$\frac{1}{3}$x+1过点B且与y轴交于点D,E为抛物线顶点.若∠DBC=α,∠CBE=β,
如图,抛物线y=ax2+bx-3与x轴交于A、B两点,与y轴交于点C,且OB=OC=3OA.直线y=-$\frac{1}{3}$x+1过点B且与y轴交于点D,E为抛物线顶点.若∠DBC=α,∠CBE=β,