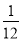��Ŀ����
��ͼ��������m��y=��0.25��x+h��2+k��x��Ľ���ΪA��B����y��Ľ���ΪC������ΪM��3��6.25������������m�Ƶ�B��ת180�㣬�õ��µ�������n�����Ķ���ΪD��
��1����������n�Ľ���ʽ��
��2����������n��x�����һ������ΪE����P���߶�DE��һ�����㣨P����D��E�غϣ�������P��y��Ĵ��ߣ�����ΪF������EF�����P�������Ϊ��x��y������PEF�����ΪS����S��x�ĺ�����ϵʽ��д���Ա���x��ȡֵ��Χ�������S�����ֵ��
��3����������m�ĶԳ�����x��Ľ���ΪG����GΪԲ�ģ�A��B�����ľ���Ϊֱ������G�����ж�ֱ��CM���G��λ�ù�ϵ����˵�����ɣ�
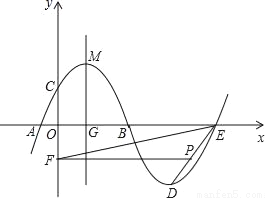
��ϰ��ϵ�д�
 ���ѵ����Ԫ��ĩ���100��ϵ�д�
���ѵ����Ԫ��ĩ���100��ϵ�д� ��˼άС�ھ�100����ҵ��ϵ�д�
��˼άС�ھ�100����ҵ��ϵ�д� ��ʦָ��һ��ͨϵ�д�
��ʦָ��һ��ͨϵ�д�
�����Ŀ


 ��[4��(��5)2]
��[4��(��5)2]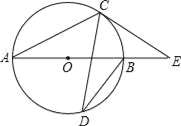
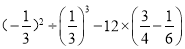
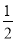 B.
B. 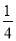 C.
C. 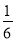 D.
D.