题目内容
16.直角三角形斜边为$\sqrt{6}$,周长是3+$\sqrt{6}$,则三角形面积为$\frac{3}{4}$.分析 设出直角三角形的两直角边分别为x与y,再由斜边的长及已知三角形的周长,利用勾股定理以及周长的定义得到x和y的两个关系式,然后利用完全平方公式即可求得xy的值,然后根据三角形的面积等于$\frac{1}{2}$xy即可求解.
解答 解:设直角三角形的两直角边分别为x和y,
∵直角三角形的斜边长是$\sqrt{6}$,
∴x2+y2=6…①,
∵周长是3+$\sqrt{6}$,
∴x+y+$\sqrt{6}$=3+$\sqrt{6}$,即x+y=3…②
将②左右两边平方得:(x+y)2=x2+2xy+y2=9,
将①代入得:2xy+6=9,即xy=$\frac{3}{2}$,
则此三角形的面积S=$\frac{1}{2}$xy=$\frac{1}{2}$×$\frac{3}{2}$=$\frac{3}{4}$.
故答案是:$\frac{3}{4}$.
点评 此题考查了勾股定理,完全平方公式的应用,以及直角三角形面积的求法,利用了方程及整体代入的思想,是中考中常考的题型.

练习册系列答案
 优等生题库系列答案
优等生题库系列答案
相关题目
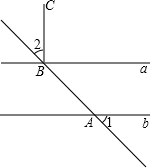 如图直线a∥b,直线c分别交直线a、b于点A、B两点,CB⊥b于点B,若∠1=60°,则∠2=30°.
如图直线a∥b,直线c分别交直线a、b于点A、B两点,CB⊥b于点B,若∠1=60°,则∠2=30°.