题目内容
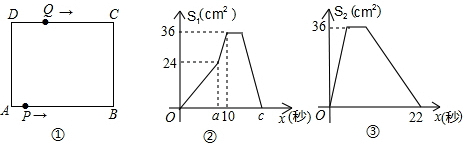
如图1,在矩形ABCD中,AB=12cm,BC=6cm,点P从A点出发,沿A→B→C→D路线运动,到D点停止;点Q从D点出发,沿D→C→B→A运动,到A点停止.若点P、点Q同时出发,点P的速度为每秒1cm,点Q的速度为每秒2cm,a秒时点P、点Q同时改变速度,点P的速度变为每秒b(cm),点Q的速度变为每秒c(cm).如图2是点P出发x秒后△APD的面积S1(cm2)与x(秒)的函数关系图象;图3是点Q出发x秒后△AQD的面积S2(cm2)与x(秒)的函数关系图象.根据图象:
(1)求a、b、c的值;
(2)设点P出发x(秒)后离开点A的路程为y(cm),请写出y与x的函数关系式,并求出点P与Q相遇时x的值.
(1)求a、b、c的值;
(2)设点P出发x(秒)后离开点A的路程为y(cm),请写出y与x的函数关系式,并求出点P与Q相遇时x的值.

考点:动点问题的函数图象
专题:
分析:(1)根据题意和S△APD求出a,b,c的值;
(2)首先求出y,y′关于x的等量关系,然后根据题意可得y=y′求出x的值.
(2)首先求出y,y′关于x的等量关系,然后根据题意可得y=y′求出x的值.
解答:解:(1)观察图象得,S△APD=
PA•AD=
×(1×a)×6=24,
解得a=8(秒)
b=
=2(厘米/秒)
(22-8)c=(12×2+6)-2×8
解得c=1(厘米/秒)
(2)依题意得:y=1×8+2(x-8),即y=2x-8(x>8).
设点Q到点A还需要走的路程为y′(cm),则
y′=(30-2×8)-1×(x-8)
=22-x(x>8)
又据题意,当y=y′时,P与Q相遇,即
2x-8=22-x,
解得x=10(秒)
∴出发10秒时,P与Q相遇.
| 1 |
| 2 |
| 1 |
| 2 |
解得a=8(秒)
b=
| 12-1×8 |
| 10-8 |
(22-8)c=(12×2+6)-2×8
解得c=1(厘米/秒)
(2)依题意得:y=1×8+2(x-8),即y=2x-8(x>8).
设点Q到点A还需要走的路程为y′(cm),则
y′=(30-2×8)-1×(x-8)
=22-x(x>8)
又据题意,当y=y′时,P与Q相遇,即
2x-8=22-x,
解得x=10(秒)
∴出发10秒时,P与Q相遇.
点评:本题考查的是一次函数与图象的综合运用,主要考查一次函数的基本性质和函数的图象,难度中等.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
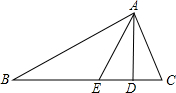 如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.
如图,在△ABC中,AD是高,AE是角平分线,∠B=20°,∠C=60°.

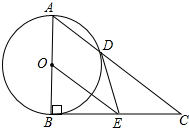 如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.
如图,Rt△ABC中,∠ABC=90°,以AB为直径的⊙O交AC于点D,E是BC的中点,连接DE、OE.