题目内容
13.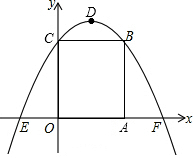 如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(2,0)、(0,3),抛物线y=-x2+bx+c经过B、C两点,交x轴于点E和点F,动点P从点E出发,以每秒1个单位的速度沿E→O→C→B向点B运动,动点Q从点B出发,以相同的速度沿B→A→F运动,到点F后,继续沿x轴正方向运动,当点P到达点B时点Q随之停止运动.
如图,在平面直角坐标系中,矩形OABC的顶点A、C的坐标分别为(2,0)、(0,3),抛物线y=-x2+bx+c经过B、C两点,交x轴于点E和点F,动点P从点E出发,以每秒1个单位的速度沿E→O→C→B向点B运动,动点Q从点B出发,以相同的速度沿B→A→F运动,到点F后,继续沿x轴正方向运动,当点P到达点B时点Q随之停止运动.(1)求抛物线所对应的函数关系式
(2)设点P的运动时间为t(秒),试探究是否存在这样的t,使点P、Q所在的直线将矩形OABC分成面积相等的两部分,若存在,求出t的值;若不存在,请说明理由
(3)设抛物线的顶点为D,求出当△DPQ为等腰三角形时t的值
(4)直接写出以P、Q、C、F为顶点的四边形为轴对称图形或中心对称图形时t的取值范围.
分析 (1)利用待定系数法即可解决问题.
(2)分四种情形讨论①如图当点P在OE上时,矩形的对角线AC与OB交于点H,则H(1,$\frac{3}{2}$).求出直线PQ的解析式(用t表示),然后利用待定系数法解决.②当点P在线段OC上,点Q在线段AB上时,直线PQ不可能经过点H,此时不存在.③当点P在线段OC上,点Q在射线AF上时,方法类似①,④当点P在线段BC上时,显然直线PQ不经过点H,此时不存在.
(3)分两种情形①如图3中,当DP=QD时,△DPQ是等腰三角形.②如图3中,当PD=PQ时,△PQD是等腰三角形.分别列出方程即可解决.
(4)分两种情形①如图4中,当点Q与点A重合时,OP=OA,易知四边形PCFQ是等腰梯形,是轴对称图形,②如图5中,当点Q在线段BC上时,易知四边形CPQF是平行四边形,是中心对称图形,即可解决问题.
解答 解:(1)∵抛物线抛y=-x2+bx+c经过B、C两点经过C(0,3),B(2,3),
∴$\left\{\begin{array}{l}{c=3}\\{-4+2b+c=3}\end{array}\right.$,解得$\left\{\begin{array}{l}{b=2}\\{c=3}\end{array}\right.$,
∴抛物线的解析式为y=-x2+2x+3,
(2)①如图当点P在OE上时,矩形的对角线AC与OB交于点H,则H(1,$\frac{3}{2}$).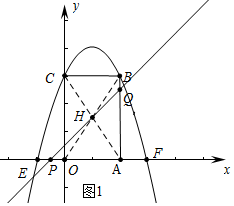
∵P(t-1,0),Q(2,3-t),
∴直线PQ的解析式为y=x+1-t,
当直线PQ经过点H时,直线PQ平分矩形ABCD的面积,
∴$\frac{3}{2}$=1+1-t,
∴t=$\frac{1}{2}$.
②当点P在线段OC上,点Q在线段AB上时,直线PQ不可能经过点H,此时不存在.
③当点P在线段OC上,点Q在射线AF上时,
∵P(0,t-1),Q(2+t-3,0),
∴直线PQ的解析式为y=-x+t-1,
当直线PQ经过点H时,直线PQ平分矩形ABCD的面积,
∴$\frac{3}{2}$=-1+t-1,
∴t=$\frac{7}{2}$,
④当点P在线段BC上时,显然直线PQ不经过点H,此时不存在.
综上所述,当t=$\frac{1}{2}$s或$\frac{7}{2}$s时,直线PQ平分矩形ABCD的面积.
(3)①如图3中,当DP=QD时,△DPQ是等腰三角形.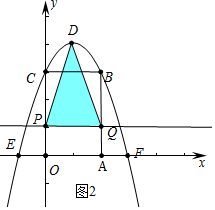
根据对称性可知,PC=BQ,
∴4-t=t,
∴t=2.
②如图3中,当PD=PQ时,△PQD是等腰三角形.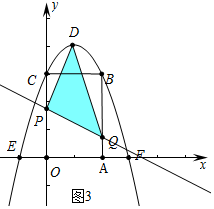
∵D(1,4),P(0,t-1),Q(2,3-t),
∴12+(t-5)2=22+(4-t+3-t)2,
∴t=3.
综上所述,t=2或3时,△DPQ是等腰三角形.
(4)①如图4中,当点Q与点A重合时,OP=OA,易知四边形PCFQ是等腰梯形,是轴对称图形,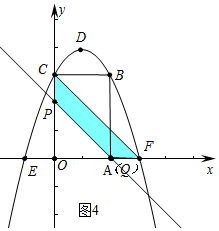
当点Q在射线AF上时,OP=OQ=t-1,四边形PCFQ是等腰梯形,
∴3≤t≤4时,四边形PCQF是轴对称图形.
②如图5中,当点Q在线段BC上时,易知四边形CPQF是平行四边形,是中心对称图形,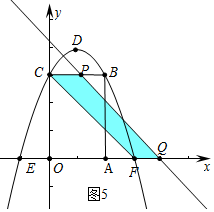
∴4<t≤6时,四边形CPQF是中心对称图形.
综上所述,3≤t≤6时,以P、Q、C、F为顶点的四边形为轴对称图形或中心对称图形.
点评 本题考查二次函数综合题、一次函数的应用、矩形的性质、等腰三角形的判定和性质,轴对称图形、中心对称图形的性质等知识,解题的关键是灵活运用所学知识,学会用分类讨论的思想思考问题,学会利用图象解决问题,体现了数形结合的思想,属于中考压轴题.

| A. | 两个锐角的和一定是钝角 | |
| B. | 两条平行线被第三条直线所截,同旁内角的平分线互相垂直 | |
| C. | 两条直线被第三条直线所截,同旁内角互补 | |
| D. | 直线外一点到这条直线的垂线段,叫做这点到该直线的距离 |
| A. | 当x<2,y随x的增大而减小 | B. | 函数的对称轴是直线x=1 | ||
| C. | 函数的开口方向向上 | D. | 函数图象与y轴的交点坐标是(0,-3) |

(1)根据上图中提供的数据填写表:
| 平均成绩(分) | 中位数(分) | 众数(分) | 方差(S2) | |
| A同学 | 80 | 80 | 80 | 60 |
| B同学 | 80 | 85 | 90 | 260 |
(3)根据图表信息,请你对A,B两位同学各提一条不超过20字的学习建议.
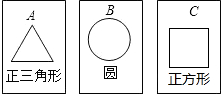 如图,有三张背面完全相同的纸牌A、B、C,其中正面分别画有三种不同的几何图形,小华将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张,请你用画树状图或列表的方法,求摸出的两张纸牌面上所画几何图形既是轴对称图形又是中心对称图形的概率.
如图,有三张背面完全相同的纸牌A、B、C,其中正面分别画有三种不同的几何图形,小华将这3张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸出一张,请你用画树状图或列表的方法,求摸出的两张纸牌面上所画几何图形既是轴对称图形又是中心对称图形的概率.