题目内容
12.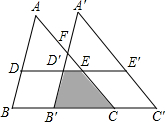 如图,在△ABC中,BC=5,D、E分别是AB、AC上的点,连接DE,有DE=3且DE∥BC,现有将△ABC沿BC平移一段距离得到△A′B′C′,A′B′与AC交于点F,并测得∠A′FE=131°,D,E的对应点分别是D′,E′,3S四边形B′CED′=S四边形BC′E′D,则下列说法不正确的是( )
如图,在△ABC中,BC=5,D、E分别是AB、AC上的点,连接DE,有DE=3且DE∥BC,现有将△ABC沿BC平移一段距离得到△A′B′C′,A′B′与AC交于点F,并测得∠A′FE=131°,D,E的对应点分别是D′,E′,3S四边形B′CED′=S四边形BC′E′D,则下列说法不正确的是( )| A. | ∠A=49° | B. | 四边形CC′E′E是平行四边形 | ||
| C. | B′C=DE | D. | S△ABC=5S△D′FE |
分析 根据平移的性质得到AC∥A′C′,∠A=∠A′,则利用平行线的性质可计算出∠A′=49°,则∠A=49°;加+x)•h,解得x=2,B′C=3,则B′C=DE;设点F与DE的距离为h′,点A到BC的距离为h1,根据平行线分线段成比例定理,由D′E∥B′C,$\frac{h′}{h′+h}$=$\frac{D′E}{B′C}$=$\frac{1}{7}$,则h=6h′,由DE∥BC得到$\frac{{h}_{1}-h}{{h}_{1}}$=$\frac{DE}{BC}$=$\frac{3}{5}$,则h=$\frac{2}{5}$h1,所以h′=$\frac{1}{15}$h1,然后根据三角形面积公式得到$\frac{{S}_{△FDE}}{{S}_{△ABC}}$=$\frac{\frac{1}{2}DE•h′}{\frac{1}{2}BC•{h}_{1}}$=$\frac{1}{25}$.
解答 解:∵△ABC沿BC平移一段距离得到△A′B′C′,
∴AC∥A′C′,∠A=∠A′,
∴∠A′+∠A′FE=180°,
∴∠A′=180°-131°=49°,
∴∠A=49°,所以A选项的说法正确;
∵DE∥BC,
∴四边形CC′E′E是平行四边形,所以B选项的说法正确;
设BB′=x,DE与BC的距离为h,则DD′=x,B′C=5-x,BC′=5+x,DE′=3+x,D′E=3-x,
∵3S四边形B′CED′=S四边形BC′E′D,
∴3•$\frac{1}{2}$(3-x+5-x)•h=$\frac{1}{2}$(3+x+5+x)•h,解得x=2,
∴B′C=5-2=3,
∴B′C=DE,所以C选项的说法正确;
设点F与DE的距离为h′,点A到BC的距离为h1,
∵D′E∥B′C,
∴$\frac{h′}{h′+h}$=$\frac{D′E}{B′C}$=$\frac{3-\frac{8}{3}}{\frac{7}{3}}$=$\frac{1}{7}$,
∴h=6h′,
∵DE∥BC,
∴$\frac{{h}_{1}-h}{{h}_{1}}$=$\frac{DE}{BC}$=$\frac{3}{5}$,
∴h=$\frac{2}{5}$h1,
∴$\frac{2}{5}$h1=6h′,即h′=$\frac{1}{15}$h1,
∴$\frac{{S}_{△FDE}}{{S}_{△ABC}}$=$\frac{\frac{1}{2}DE•h′}{\frac{1}{2}BC•{h}_{1}}$=$\frac{3•\frac{1}{15}{h}_{1}}{5•{h}_{1}}$=$\frac{1}{25}$,所以D选项的说法错误.
故选D.
点评 本题考查了平移的性质:把一个图形整体沿某一直线方向移动,会得到一个新的图形,新图形与原图形的形状和大小完全相同. ②新图形中的每一点,都是由原图形中的某一点移动后得到的,这两个点是对应点.连接各组对应点的线段平行且相等.也考查了平行线分线段成比例定理.

 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案| A. | y=4x | B. | $\frac{y}{x}$=3 | C. | y=6x+1 | D. | xy=2 |
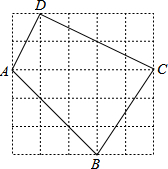 如图,每个小方格都是边长为1的正方形.
如图,每个小方格都是边长为1的正方形.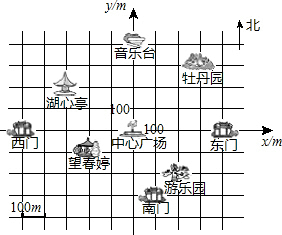 如图,这是人民公园的景区示意图.以中心广场为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,规定一个单位长度代表100m长.已知各建筑物都在坐标平面网格的格点上,且东门的坐标为(400,0).
如图,这是人民公园的景区示意图.以中心广场为原点,分别以正东、正北方向为x轴、y轴正方向建立平面直角坐标系,规定一个单位长度代表100m长.已知各建筑物都在坐标平面网格的格点上,且东门的坐标为(400,0).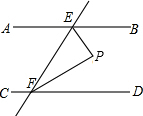 已知:如图,直线EF分别交AB,CD于点E,F,且∠AEF=66°,∠BEF的平分线与∠DFE的平分线相交于点P.
已知:如图,直线EF分别交AB,CD于点E,F,且∠AEF=66°,∠BEF的平分线与∠DFE的平分线相交于点P.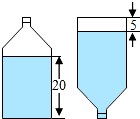 有种饮料瓶如图,它的直径是4cm,里面的水高度是20cm,把瓶盖拧紧倒置放平,无水部分圆柱高度是5cm,求饮料瓶的容积是多少?(结果保留整数)
有种饮料瓶如图,它的直径是4cm,里面的水高度是20cm,把瓶盖拧紧倒置放平,无水部分圆柱高度是5cm,求饮料瓶的容积是多少?(结果保留整数)