题目内容
20.计算:(1)${(-\sqrt{10})}^{2}$-$\sqrt{(-7)^{2}}$+$\sqrt{\frac{1}{2}}$;
(2)${(\sqrt{2}+1)}^{2}$-($\sqrt{2}$+1).
分析 (1)根据二次根式的性质化简后合并即可;
(2)先利用完全平方公式计算,然后合并即可.
解答 解:(1)原式=10-7+$\frac{\sqrt{2}}{2}$
=3+$\frac{\sqrt{2}}{2}$;
(2)原式=2+2$\sqrt{2}$+1-$\sqrt{2}$-1
=2+$\sqrt{2}$.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.

练习册系列答案
相关题目
12.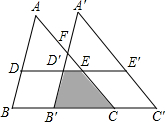 如图,在△ABC中,BC=5,D、E分别是AB、AC上的点,连接DE,有DE=3且DE∥BC,现有将△ABC沿BC平移一段距离得到△A′B′C′,A′B′与AC交于点F,并测得∠A′FE=131°,D,E的对应点分别是D′,E′,3S四边形B′CED′=S四边形BC′E′D,则下列说法不正确的是( )
如图,在△ABC中,BC=5,D、E分别是AB、AC上的点,连接DE,有DE=3且DE∥BC,现有将△ABC沿BC平移一段距离得到△A′B′C′,A′B′与AC交于点F,并测得∠A′FE=131°,D,E的对应点分别是D′,E′,3S四边形B′CED′=S四边形BC′E′D,则下列说法不正确的是( )
 如图,在△ABC中,BC=5,D、E分别是AB、AC上的点,连接DE,有DE=3且DE∥BC,现有将△ABC沿BC平移一段距离得到△A′B′C′,A′B′与AC交于点F,并测得∠A′FE=131°,D,E的对应点分别是D′,E′,3S四边形B′CED′=S四边形BC′E′D,则下列说法不正确的是( )
如图,在△ABC中,BC=5,D、E分别是AB、AC上的点,连接DE,有DE=3且DE∥BC,现有将△ABC沿BC平移一段距离得到△A′B′C′,A′B′与AC交于点F,并测得∠A′FE=131°,D,E的对应点分别是D′,E′,3S四边形B′CED′=S四边形BC′E′D,则下列说法不正确的是( )| A. | ∠A=49° | B. | 四边形CC′E′E是平行四边形 | ||
| C. | B′C=DE | D. | S△ABC=5S△D′FE |
9.设A(-3,y1),B(0,y2),C(1,y3)是抛物线y=-(x+1)2+m上的三点,则y1,y2,y3的大小关系为( )
| A. | y1=y2>y3 | B. | y1=y3<y2 | C. | y1=y3=y2 | D. | y1>y2>y3 |
 如图,点A关于x轴的对称点的坐标是(5,3).
如图,点A关于x轴的对称点的坐标是(5,3). 如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,点B在二次函数y=$\frac{1}{8}$x2+bx+c的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.
如图,△ABC是以BC为底边的等腰三角形,点A、C分别是一次函数y=-$\frac{3}{4}$x+3的图象与y轴、x轴的交点,点B在二次函数y=$\frac{1}{8}$x2+bx+c的图象上,且该二次函数图象上存在一点D使四边形ABCD能构成平行四边形.