题目内容
16.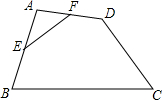 如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC等于( )
如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
分析 连接BD,根据中位线的性质得出EF∥BD,且EF=$\frac{1}{2}$BD,进而利用勾股定理的逆定理得出△BDC是直角三角形,求解即可.
解答 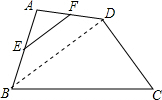 解:连接BD,
解:连接BD,
∵E、F分别是AB、AD的中点,
∴EF∥BD,且EF=$\frac{1}{2}$BD,
∵EF=4,
∴BD=8,
∵BD=8,BC=10,CD=6,
∴82+62=102,即BD2+CD2=BC2,
∴△BDC是直角三角形,且∠BDC=90°,
∴tanC=$\frac{BD}{DC}$=$\frac{8}{6}$=$\frac{4}{3}$,
故选:A.
点评 此题主要考查了锐角三角形的定义以及三角形中位线的性质以及勾股定理逆定理,根据已知得出△BDC是直角三角形是解题关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
4.由下列条件不能判定△ABC为直角三角形的是( )
| A. | ∠A+∠B=∠C | B. | ∠A:∠B:∠C=1:3:2 | ||
| C. | (b+c)(b-c)=a2 | D. | a=3+k,b=4+k,c=5+k(k>0) |
8.一次中学生田径运动会上,参加男子跳高的20名运动员成绩如下所示:
则下列叙述正确的是( )
| 成绩(单位:米) | 1.50 | 1.60 | 1.65 | 1.70 | 1.75 | 1.80 | 1.85 | 1.90 |
| 人数 | 2 | 3 | 2 | 4 | 5 | 2 | 1 | 1 |
| A. | 这些运动员成绩的中位数是1.70 | B. | 这些运动员成绩的众数是5 | ||
| C. | 这些运动员的平均成绩是1.71875 | D. | 这些运动员成绩的方差是0.0725 |
5.$\frac{{\sqrt{5}}}{2}$是( )
| A. | 分数 | B. | 有理数 | C. | 小数 | D. | 整数 |
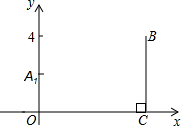 如图,已知两点A (0,2)、B(9,4),BC⊥x轴于C,若线段OC上的点P使以AOP为顶点的三角形与△BCP相似,则点P的横坐标为1或3或8.
如图,已知两点A (0,2)、B(9,4),BC⊥x轴于C,若线段OC上的点P使以AOP为顶点的三角形与△BCP相似,则点P的横坐标为1或3或8. 如图是由几个相同的小正方体所搭几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,则这个几何体的左视图是( )
如图是由几个相同的小正方体所搭几何体的俯视图,小正方形中的数字表示在该位置的小正方体的个数,则这个几何体的左视图是( )



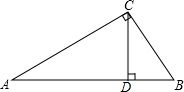 如图,Rt△ABC的斜边AB=1,∠B=α,CD⊥AB,垂足为D点.
如图,Rt△ABC的斜边AB=1,∠B=α,CD⊥AB,垂足为D点.