题目内容
4.由下列条件不能判定△ABC为直角三角形的是( )| A. | ∠A+∠B=∠C | B. | ∠A:∠B:∠C=1:3:2 | ||
| C. | (b+c)(b-c)=a2 | D. | a=3+k,b=4+k,c=5+k(k>0) |
分析 由勾股定理的逆定理,只要验证两小边的平方和等于最长边的平方或最大角是否是90°即可判断△ABC是否为直角三角形.
解答 解:A、∵∠A+∠B=∠C,∴∠C=90°,是直角三角形,故此选项错误;
B、∵∠A:∠B:∠C=1:3:2,∴∠B=$\frac{3}{6}$×180°=90°,是直角三角形,故此选项错误;
C、∵(b+c)(b-c)=a2,∴b2-c2=a2,即a2+c2=b2,是直角三角形,故此选项错误;
D、∵a2+b2≠c2,∴此三角形不是直角三角形,故此选项正确.
故选D.
点评 本题考查勾股定理的逆定理的应用.判断三角形是否为直角三角形,已知三角形三边的长,只要利用勾股定理的逆定理加以判断即可.

练习册系列答案
相关题目
15.分解因式m-ma2的结果是( )
| A. | m(1+a)(1-a) | B. | m(1+a)2 | C. | m(1-a)2 | D. | (1-a)(1+a) |
12.已知实数a,b,若a>b,则下列结论正确的是( )
| A. | a-2<b-2 | B. | 2+a<2+b | C. | $\frac{a}{2}$<$\frac{b}{2}$ | D. | -2a<-2b |
19.-$\frac{1}{2015}$的相反数是( )
| A. | -$\frac{1}{2015}$ | B. | $\frac{1}{2015}$ | C. | 2015 | D. | -2015 |
16.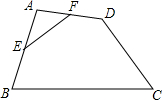 如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC等于( )
如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC等于( )
 如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC等于( )
如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
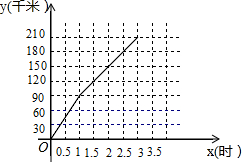 甲车由A地出发沿一条公路向B地行驶,3小时到达.甲车行驶的路程y(千米)与所用时间x(时)之间的函数图象如图所示.
甲车由A地出发沿一条公路向B地行驶,3小时到达.甲车行驶的路程y(千米)与所用时间x(时)之间的函数图象如图所示.