题目内容
6.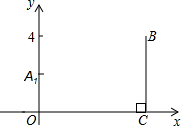 如图,已知两点A (0,2)、B(9,4),BC⊥x轴于C,若线段OC上的点P使以AOP为顶点的三角形与△BCP相似,则点P的横坐标为1或3或8.
如图,已知两点A (0,2)、B(9,4),BC⊥x轴于C,若线段OC上的点P使以AOP为顶点的三角形与△BCP相似,则点P的横坐标为1或3或8.
分析 由A (0,2)、B(9,4),可得OA=2,BC=4,OC=9,然后设OP=x,则PC=9-x,再分别从当△AOP∽△PCB时,$\frac{AO}{PC}=\frac{OP}{BC}$与当△AOP∽△BCP时,$\frac{AO}{BC}=\frac{OP}{CP}$,去分析求解即可求得答案.
解答 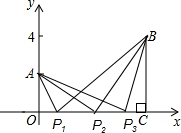 解:∵A (0,2)、B(9,4),
解:∵A (0,2)、B(9,4),
∴OA=2,BC=4,OC=9,
设OP=x,则PC=9-x,
①当△AOP∽△PCB时,$\frac{AO}{PC}=\frac{OP}{BC}$,
∴$\frac{2}{9-x}=\frac{x}{4}$,
解得:x1=1,x2=8,
∴点P的横坐标为1或8;
②当△AOP∽△BCP时,$\frac{AO}{BC}=\frac{OP}{CP}$,
∴$\frac{2}{4}=\frac{x}{9-x}$,
解得:x=3,
∴点P的横坐标为3;
综上:点P的横坐标为1或3或8.
故答案为:1或3或8.
点评 此题考查了相似三角形的判定.注意分类讨论思想的应用.

练习册系列答案
 名师指导期末冲刺卷系列答案
名师指导期末冲刺卷系列答案
相关题目
17. 如图,自行车的车身为三角结构,这是因为三角形具有( )
如图,自行车的车身为三角结构,这是因为三角形具有( )
 如图,自行车的车身为三角结构,这是因为三角形具有( )
如图,自行车的车身为三角结构,这是因为三角形具有( )| A. | 对称性 | B. | 稳定性 | C. | 全等性 | D. | 以上都是 |
1.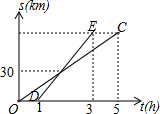 已知甲乙两人沿同一条公路从A地到B地,图中线段OC,DE分别表示甲乙从离开A地到达B地的过程中路程s(单位:km)与时间t(单位h)的函数关系,则从A地到B地的路程为( )
已知甲乙两人沿同一条公路从A地到B地,图中线段OC,DE分别表示甲乙从离开A地到达B地的过程中路程s(单位:km)与时间t(单位h)的函数关系,则从A地到B地的路程为( )
 已知甲乙两人沿同一条公路从A地到B地,图中线段OC,DE分别表示甲乙从离开A地到达B地的过程中路程s(单位:km)与时间t(单位h)的函数关系,则从A地到B地的路程为( )
已知甲乙两人沿同一条公路从A地到B地,图中线段OC,DE分别表示甲乙从离开A地到达B地的过程中路程s(单位:km)与时间t(单位h)的函数关系,则从A地到B地的路程为( )| A. | 60km | B. | 80km | C. | 90km | D. | 120km |
11.某品牌服装折扣店将某件衣服按进价提高30%后标价,再打9折(标价的90%)销售,售价为240元,设这件衣服的进价为x元,根据题意,下面所列的方程正确的是( )
| A. | x•30%×90%=240 | B. | x•(1+30%)×90%=240 | C. | 240×30%×90%=x | D. | x•(1+30%)=240×90% |
15.分解因式m-ma2的结果是( )
| A. | m(1+a)(1-a) | B. | m(1+a)2 | C. | m(1-a)2 | D. | (1-a)(1+a) |
16.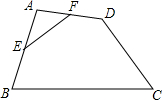 如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC等于( )
如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC等于( )
 如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC等于( )
如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
 如图:在三角形ABC中,AB=AC,D在AC上,且BD=BC=AD,则△ABC各内角中,∠A=36°;∠ABC=72°;∠C=72°.
如图:在三角形ABC中,AB=AC,D在AC上,且BD=BC=AD,则△ABC各内角中,∠A=36°;∠ABC=72°;∠C=72°.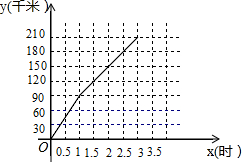 甲车由A地出发沿一条公路向B地行驶,3小时到达.甲车行驶的路程y(千米)与所用时间x(时)之间的函数图象如图所示.
甲车由A地出发沿一条公路向B地行驶,3小时到达.甲车行驶的路程y(千米)与所用时间x(时)之间的函数图象如图所示.