题目内容
1.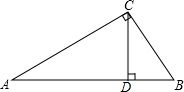 如图,Rt△ABC的斜边AB=1,∠B=α,CD⊥AB,垂足为D点.
如图,Rt△ABC的斜边AB=1,∠B=α,CD⊥AB,垂足为D点.(1)用含α三角函数表示线段BD、CD、AD的长度;
(2)通过你的计算的结果或者运算过程,你发现了哪些有关于三角函数的性质或者三角函数的等式?请举一例即可.
分析 (1)在Rt△ABC中,根据三角函数的定义得出BC=AB•cosα=cosα,AC=AB•sinα=sinα.在Rt△BCD中,根据三角函数的定义得出BD=BC•cosα=cos2α;CD=BC•sinα=sinαcosα;由同角的余角相等得出∠ACD=∠B=90°-∠BCD=α,在Rt△ACD中,根据三角函数的定义得出AD=AC•sin∠ACD=sin2α;
(2)由AD+BD=AB得出sin2α+cos2α=1;由tan∠B=$\frac{AC}{BC}$得出tanα=$\frac{sinα}{cosα}$.
解答 解:(1)∵Rt△ABC的斜边AB=1,∠B=α,
∴BC=AB•cosα=cosα,AC=AB•sinα=sinα.
在Rt△BCD中,∵∠BDC=90°,
∴BD=BC•cosα=cosα•cosα=cos2α;
CD=BC•sinα=sinαcosα;
在Rt△ACD中,∵∠ADC=90°,∠ACD=∠B=90°-∠BCD=α,
∴AD=AC•sin∠ACD=sinα•sinα=sin2α;
(2)∵AD+BD=AB,
∴sin2α+cos2α=1;
∵在Rt△ABC中,tan∠B=$\frac{AC}{BC}$,
∴tanα=$\frac{sinα}{cosα}$.
点评 本题考查了解直角三角形,熟练掌握锐角三角函数的定义是解题的关键.也考查了同角的余角相等的性质.

练习册系列答案
相关题目
11.某品牌服装折扣店将某件衣服按进价提高30%后标价,再打9折(标价的90%)销售,售价为240元,设这件衣服的进价为x元,根据题意,下面所列的方程正确的是( )
| A. | x•30%×90%=240 | B. | x•(1+30%)×90%=240 | C. | 240×30%×90%=x | D. | x•(1+30%)=240×90% |
12.已知实数a,b,若a>b,则下列结论正确的是( )
| A. | a-2<b-2 | B. | 2+a<2+b | C. | $\frac{a}{2}$<$\frac{b}{2}$ | D. | -2a<-2b |
16.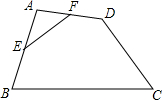 如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC等于( )
如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC等于( )
 如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC等于( )
如图,在四边形ABCD中,E、F分别是AB、AD的中点,若EF=4,BC=10,CD=6,则tanC等于( )| A. | $\frac{4}{3}$ | B. | $\frac{3}{4}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |