题目内容
19. 如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(-3,-1)和点B(0,2).
如图,在平面直角坐标系xOy中,一次函数y=kx+b的图象经过点A(-3,-1)和点B(0,2).(1)求一次函数的表达式;
(2)若点P在y轴上,且PB=$\frac{1}{2}$BO,直接写出点P的坐标.
分析 (1)用待定系数法求一次函数的解析式即可;
(2)根据点P在y轴上,设P(0,m),再求得OB,根据PB=$\frac{1}{2}$BO,得出点P的坐标即可.
解答  (1)解:∵一次函数的图象经过点A(-3,-1)和点B(0,2),
(1)解:∵一次函数的图象经过点A(-3,-1)和点B(0,2),
∴$\left\{\begin{array}{l}{-1=-3k+b}\\{b=2}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=1}\\{b=2}\end{array}\right.$
∴一次函数的表达式为y=x+2;
(2)设P(0,m),
∵B(0,2),
∴OB=2,PB=|m-2|,
∵PB=$\frac{1}{2}$BO,
∴m=1或m=3,
∴P(0,1)或(0,3).
点评 本题考查了用待定系数法求一次函数的解析式,掌握方程组的解法是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.下列式子一定是二次根式的是( )
| A. | $\sqrt{x-1}$ | B. | $\sqrt{x}$ | C. | $\sqrt{{x}^{2}+2}$ | D. | $\sqrt{{x}^{2}-2}$ |
10.已知关于x的不等式组$\left\{\begin{array}{l}{x-a≥b}\\{2x-a<2b+1}\end{array}\right.$的解集为3≤x<5,则a、b的值分别为( )
| A. | -3,6 | B. | 6,-3 | C. | 1,2 | D. | 0,3 |
7.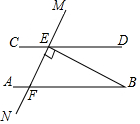 如图所示:AB∥CD,MN交CD于点E,交AB于F,BE⊥MN于点E,若∠DEM=55°,则∠ABE=( )
如图所示:AB∥CD,MN交CD于点E,交AB于F,BE⊥MN于点E,若∠DEM=55°,则∠ABE=( )
 如图所示:AB∥CD,MN交CD于点E,交AB于F,BE⊥MN于点E,若∠DEM=55°,则∠ABE=( )
如图所示:AB∥CD,MN交CD于点E,交AB于F,BE⊥MN于点E,若∠DEM=55°,则∠ABE=( )| A. | 55° | B. | 35° | C. | 45° | D. | 30° |
14.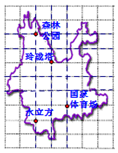 “健步走”越来越受到人们的喜爱,某个“健步走”小组将自己的活动场地定在奥林匹克公园,所走路线如图所示:森林公园-玲珑塔-国家体育场-水立方.设在奥林匹克公园设计图上玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),那么,水立方的坐标为( )
“健步走”越来越受到人们的喜爱,某个“健步走”小组将自己的活动场地定在奥林匹克公园,所走路线如图所示:森林公园-玲珑塔-国家体育场-水立方.设在奥林匹克公园设计图上玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),那么,水立方的坐标为( )
 “健步走”越来越受到人们的喜爱,某个“健步走”小组将自己的活动场地定在奥林匹克公园,所走路线如图所示:森林公园-玲珑塔-国家体育场-水立方.设在奥林匹克公园设计图上玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),那么,水立方的坐标为( )
“健步走”越来越受到人们的喜爱,某个“健步走”小组将自己的活动场地定在奥林匹克公园,所走路线如图所示:森林公园-玲珑塔-国家体育场-水立方.设在奥林匹克公园设计图上玲珑塔的坐标为(-1,0),森林公园的坐标为(-2,2),那么,水立方的坐标为( )| A. | (-2,-4) | B. | (-1,-4) | C. | (-2,4) | D. | (-4,-1) |
4.使式子$\sqrt{x-4}$有意义的条件是( )
| A. | x≥4 | B. | x=4 | C. | x≤4 | D. | x≠4 |
11. 如图,一艘船由A港沿北偏西60°方向航行10海里至B港,然后再沿北偏东30°方向航行10海里至C港.则下列说法正确的是( )
如图,一艘船由A港沿北偏西60°方向航行10海里至B港,然后再沿北偏东30°方向航行10海里至C港.则下列说法正确的是( )
 如图,一艘船由A港沿北偏西60°方向航行10海里至B港,然后再沿北偏东30°方向航行10海里至C港.则下列说法正确的是( )
如图,一艘船由A港沿北偏西60°方向航行10海里至B港,然后再沿北偏东30°方向航行10海里至C港.则下列说法正确的是( )| A. | C港在A港的南偏西30°方向上 | B. | C港在A港的北偏西30°方向上 | ||
| C. | C港在A港的北偏西15°方向上 | D. | C港在A港的南偏西15°方向上 |
8. 如图,AB∥CD,EF分别与AB,CD相交于点E、F,则图中与∠AEF相等的角的个数有( )
如图,AB∥CD,EF分别与AB,CD相交于点E、F,则图中与∠AEF相等的角的个数有( )
 如图,AB∥CD,EF分别与AB,CD相交于点E、F,则图中与∠AEF相等的角的个数有( )
如图,AB∥CD,EF分别与AB,CD相交于点E、F,则图中与∠AEF相等的角的个数有( )| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |