题目内容
19．若分式方程$\frac{a}{x-2}$+3=$\frac{1-x}{2-x}$有增根，那么a的值为（ ）| A． | -1 | B． | 2 | C． | 1 | D． | 0 |
分析 分式方程去分母转化为整式方程，由分式方程有增根，得到x=2，代入整式方程求出a的值即可．
解答 解：去分母得：a+3x-6=x-1，
由分式方程有增根，得到x-2=0，即x=2，
把x=2代入整式方程得：a=1，
故选C
点评 此题考查了分式方程的增根，增根确定后可按如下步骤进行：①化分式方程为整式方程；②把增根代入整式方程即可求得相关字母的值．
练习册系列答案
考前必练系列答案
相关题目
9．下列有理式$\frac{x+1}{3}$，$\frac{b}{5-a}$，$\frac{x}{2}$+3y，$\frac{6}{π}$，6-$\frac{1}{m}$中，分式有（ ）个．
| A． | 1 | B． | 2 | C． | 3 | D． | 4 |
10．设A（-2，y1），B（1，y2），C（2，y3）是抛物线y=-（x+1）2+1上的三点，则y1，y2，y3的大小关系为（ ）
| A． | y1＞y2＞y3 | B． | y1＞y3＞y2 | C． | y3＞y2＞y1 | D． | y3＞y1＞y2 |
7．如果$\root{3}{a}$=a，那么a是（ ）
| A． | ±1 | B． | 1，0 | C． | ±1，0 | D． | 以上都不对 |
14．
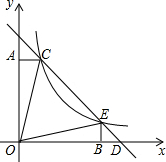如图，直线y=-x+b与反比例函数y=$\frac{k}{x}$（k≠0）的图象的一支交于C（1，4），E两点，CA⊥y轴于点A，EB⊥x轴于点B，则以下结论：
①k的值为4；
②△BED是等腰直角三角形；
③S△ACO=S△BEO；
④S△CEO=15；
⑤点D的坐标为（5，0）．其中正确的是（ ）
如图，直线y=-x+b与反比例函数y=$\frac{k}{x}$（k≠0）的图象的一支交于C（1，4），E两点，CA⊥y轴于点A，EB⊥x轴于点B，则以下结论：①k的值为4；
②△BED是等腰直角三角形；
③S△ACO=S△BEO；
④S△CEO=15；
⑤点D的坐标为（5，0）．其中正确的是（ ）
| A． | ①②③ | B． | ①②③④ | C． | ②③④⑤ | D． | ①②③⑤ |
4．计算（3a2b）3的结果是（ ）
| A． | 9a6b3 | B． | 9a2b3 | C． | 27a6b3 | D． | 27a6b |
8．下列二次根式中，最简二次根式是（ ）
| A． | $\sqrt{0.5}$ | B． | $\sqrt{15}$ | C． | $\sqrt{150}$ | D． | $\sqrt{\frac{1}{15}}$ |
9．下列二次根式中，属于最简二次根式的是（ ）
| A． | $\sqrt{4a+8}$ | B． | $\sqrt{24}$ | C． | $\sqrt{14}$ | D． | $\sqrt{1.4}$ |