题目内容
10.某校八年级(1)、(2)班参加学校“环境整洁”活动整理一批活动器材,若(1)班单独整理需要40分钟完成,现在(1)班和(2)班共同整理20分钟后,(1)班因另有任务,(2)班再单独整理了20分钟才完成任务,(2)单独整理这批实验器材需要多少分钟?分析 设(2)班单独整理这批实验器材需要x分钟,则(2)班得工作效率为$\frac{1}{x}$,而(1)班的工作效率为$\frac{1}{40}$,然后根据工作量列方程20×$\frac{1}{40}$+(20+20)×$\frac{1}{x}$=1,再解方程、检验即可得到x的值.
解答 解:设(2)班单独整理这批实验器材需要x分钟,
根据题意得20×$\frac{1}{40}$+(20+20)×$\frac{1}{x}$=1,
解得x=80,
经检验x=80是原方程的解.
答:(2)班单独整理这批实验器材需要80分钟.
点评 本题考查了分式方程的应用:列分式方程解应用题的一般步骤:设、列、解、验、答.必须严格按照这5步进行做题,规范解题步骤,另外还要注意完整性:如设和答叙述要完整,要写出单位等.要掌握常见问题中的基本关系,如行程问题:速度=路程时间;工作量问题:工作效率=工作量工作时间等等.解决本题的关键是分别表示出两班的工作效率.

练习册系列答案
 培优好卷单元加期末卷系列答案
培优好卷单元加期末卷系列答案
相关题目
19.某水果公式销售人员从所有柑橘中随机抽取若干柑橘进行“柑橘损坏率”统计,结果如下表:
估计这种柑橘损坏的概率约为0.1(精确到0.1)
| 柑橘总质量(n) | 损坏柑橘质量(m) | 柑橘损坏率(m/n) |
| 400 | 39.24 | 0.098 |
| 450 | 44.57 | 0.099 |
| 500 | 51.54 | 0.103 |
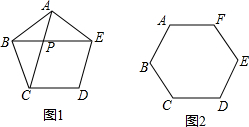
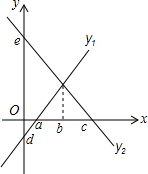 如图,先观察图形,然后填空:
如图,先观察图形,然后填空: