题目内容
16.点(2,-3)关于x轴对称的点的坐标是( )| A. | (-3,-2) | B. | (2,-3) | C. | (2,3) | D. | (-2,-3) |
分析 利用平面内两点关于x轴对称时:横坐标不变,纵坐标互为相反数,进行求解.
解答 解:点(2,-3)关于x轴对称的点的坐标是(2,3),
故选:C.
点评 本题考查了关于x轴对称的点的坐标,解决本题的关键是掌握好对称点的坐标规律:关于x轴对称的点,横坐标相同,纵坐标互为相反数;关于y轴对称的点,纵坐标相同,横坐标互为相反数;关于原点对称的点,横坐标与纵坐标都互为相反数.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
6.函数y=-x2+2x-3,顶点坐标为( )
| A. | (-1,-2) | B. | (-1,-3) | C. | (1,-3) | D. | (1,-2) |
4.下列四个图形中,既是轴对称图形又是中心对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
11.多项式1+2xy-3xy2的次数及最高次项的系数分别是( )
| A. | 5,-3 | B. | 2,-3 | C. | 3,-3 | D. | 2,3 |
8.计算:a3•a2的结果( )
| A. | a6 | B. | 5a | C. | 6a | D. | a5 |
5.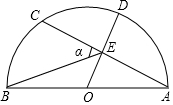 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE,设∠BEC=α,则tanα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE,设∠BEC=α,则tanα的值为( )
 如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE,设∠BEC=α,则tanα的值为( )
如图,AB是半圆的直径,点O为圆心,OA=5,弦AC=8,OD⊥AC,垂足为E,交⊙O于D,连接BE,设∠BEC=α,则tanα的值为( )| A. | $\frac{3}{2}$ | B. | $\frac{\sqrt{3}}{2}$ | C. | $\frac{5}{4}$ | D. | $\frac{2}{3}$ |
6. 如图,在△ABC中,点D,E分别在AB,AC上,则添加下面的条件后,不能判断△AED∽△ABC的是( )
如图,在△ABC中,点D,E分别在AB,AC上,则添加下面的条件后,不能判断△AED∽△ABC的是( )
 如图,在△ABC中,点D,E分别在AB,AC上,则添加下面的条件后,不能判断△AED∽△ABC的是( )
如图,在△ABC中,点D,E分别在AB,AC上,则添加下面的条件后,不能判断△AED∽△ABC的是( )| A. | $\frac{AD}{AC}$=$\frac{DE}{BC}$ | B. | $\frac{AD}{AC}$=$\frac{AE}{AB}$ | C. | ∠AED=∠B | D. | ∠ADE=∠C |
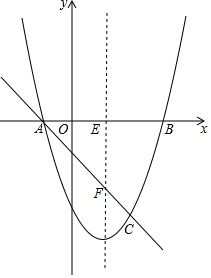 如图,抛物线y=x2-2x-3与x轴交于A、B两点(A点在B点左侧),点C为抛物线上一点,且点C的横坐标为2,抛物线的对称轴EF交x轴于点E,交直线AC于点F.
如图,抛物线y=x2-2x-3与x轴交于A、B两点(A点在B点左侧),点C为抛物线上一点,且点C的横坐标为2,抛物线的对称轴EF交x轴于点E,交直线AC于点F.