Question

11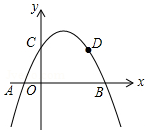．如图，二次函数y=ax²+bx+c的图象与x轴相交于A、B两点，与y轴相交于点C，其中点B坐标为B（m+2，0），若点D是该抛物线上一点，且坐标为D（m-1，c），则点A的坐标是（-3，0）．

Answer 1

分析 利用抛物线的对称性先确定出点C与D以及点A与B都关于抛物线的对称轴对称，即可．

解答 解：∵二次函数y=ax²+bx+c的图象与y轴相交于点C，
∴C（0，c），
∵D（m-1，c），
∴抛物线的对称轴为x=-$\frac{b}{2a}$=$\frac{m-1}{2}$，
∵二次函数y=ax²+bx+c的图象与x轴相交于A、B两点，
∴点A和点B关于对称轴x=-$\frac{b}{2a}$=$\frac{m-1}{2}$对称，
设A（n，0），
∴$\frac{m+2+n}{2}$=$\frac{m-1}{2}$，
∴n=-3，
∴A（-3，0），
故答案：（-3，0）．

点评 此题是抛物线与x轴的交点坐标，抛物线的对称性是解本题的关键，也是难点．