题目内容
1. 如图,已知CD是△ABC的角平分线,E是BC上的点,∠B=60°,∠ACE=∠CAE=20°.求∠CDE的度数.
如图,已知CD是△ABC的角平分线,E是BC上的点,∠B=60°,∠ACE=∠CAE=20°.求∠CDE的度数.
分析 由三角形内角和定理可求得∠BAC=100°,∠BAE=80°,AE=CE,设为1,在△ABE中,由正弦定理得BE,根据角平分线的定义和平行线的判定可得DE∥AC,进一步得到∠CDE的度数.
解答 解:∵∠B=60°,∠ACE=∠CAE=20°,
∴∠BAC=100°,∠BAE=80°,
AE=CE,设为1,
在△ABE中,由正弦定理得BE=$\frac{sin80°}{sin60°}$,
∵CD是△ABC的角平分线,
∴$\frac{AD}{DB}$=$\frac{AC}{BC}$=$\frac{sin∠ABC}{sin∠BAC}$=$\frac{sin60°}{sin100°}$=$\frac{CE}{BE}$,
∴DE∥AC,
∴∠CDE=∠ACD=10°.
点评 此题考查了三角形内角和定理,此题结合了平行线的判定和角平分线的定义,正弦定理,综合性较强,有一定的难度.

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
10.下列说法中正确的是( )
| A. | 整数都是非负数 | B. | 带有负号的数一定是负数 | ||
| C. | 分数都是有理数 | D. | 相反数是它本身的数是0和1 |
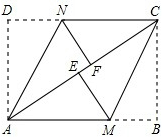 如图,在矩形ABCD中,把∠B、∠D分别翻折,使点B、D恰好落在对角线AC上的点E、F处,折痕分别为CM、AN.
如图,在矩形ABCD中,把∠B、∠D分别翻折,使点B、D恰好落在对角线AC上的点E、F处,折痕分别为CM、AN.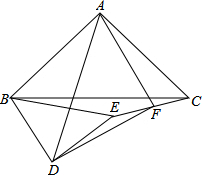 已知:如图△ABC和△BDE都是等腰直角三角形,当△BDE绕着点B转动,点F是CE的中点,求证:△ADF是等腰直角三角形.
已知:如图△ABC和△BDE都是等腰直角三角形,当△BDE绕着点B转动,点F是CE的中点,求证:△ADF是等腰直角三角形.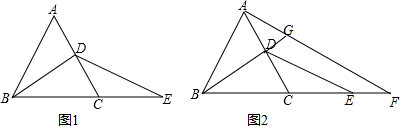
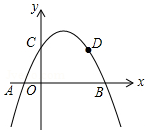 如图,二次函数y=ax2+bx+c的图象与x轴相交于A、B两点,与y轴相交于点C,其中点B坐标为B(m+2,0),若点D是该抛物线上一点,且坐标为D(m-1,c),则点A的坐标是(-3,0).
如图,二次函数y=ax2+bx+c的图象与x轴相交于A、B两点,与y轴相交于点C,其中点B坐标为B(m+2,0),若点D是该抛物线上一点,且坐标为D(m-1,c),则点A的坐标是(-3,0).