题目内容
7. 如图,在△ABC中,∠A=50°,∠ABC的平分线BP与∠ACB的平分线CP相交于点P,那么∠BPC=115°.
如图,在△ABC中,∠A=50°,∠ABC的平分线BP与∠ACB的平分线CP相交于点P,那么∠BPC=115°.
分析 根据三角形的内角和等于180°求出∠ABC+∠ACB,再根据角平分线的定义求出∠PBC+∠PCB,然后利用三角形的内角和等于180°列式计算即可得解.
解答 解:∵∠A=50°,
∴∠ABC+∠ACB=180°-50°=130°,
∵∠ABC与∠ACB的角平分线相交于P,
∴∠PBC+∠PCB=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×130°=65°,
在△PBC中,∠BPC=180°-(∠PBC+∠PCB)=180°-65°=115°.
故答案为:115°.
点评 此题考查了三角形的内角和定理,角平分线的定义,整体思想的利用是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
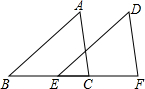 如图,已知B,E,C,F在同一条直线上,且△ABC≌△DEF,BE=3cm,则CF=3cm.
如图,已知B,E,C,F在同一条直线上,且△ABC≌△DEF,BE=3cm,则CF=3cm.