题目内容
观察下列各式:
=1-
,
=
-
,
=
-
,…,
=
-
,则
+
+
+…+
=1-
+
-
+
-
+…+
-
=1-
=
.
阅读以上解题过程,解答下列各题:
(1)计算:
+
+
+
+
+
+
;
(2)计算:
+
+
+…+
.
| 1 |
| 1×2 |
| 1 |
| 2 |
| 1 |
| 2×3 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3×4 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| n(n-1) |
| 1 |
| n |
| 1 |
| n+1 |
| 1 |
| 1×2 |
| 1 |
| 2×3 |
| 1 |
| 3×4 |
| 1 |
| 2009×2010 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 2009 |
| 1 |
| 2010 |
| 1 |
| 2010 |
| 2009 |
| 2010 |
阅读以上解题过程,解答下列各题:
(1)计算:
| 1 |
| 2 |
| 1 |
| 6 |
| 1 |
| 12 |
| 1 |
| 20 |
| 1 |
| 30 |
| 1 |
| 42 |
| 1 |
| 56 |
(2)计算:
| 1 |
| 1×5 |
| 1 |
| 5×9 |
| 1 |
| 9×13 |
| 1 |
| 2005×2009 |
考点:有理数的混合运算
专题:规律型
分析:利用计算的规律,直接拆分计算即可.
解答:解:(1)原式=1-
+
-
+
-
+…+
-
=1-
=
;
(2)原式=
×(1-
)+
×(
-
)+
×(
-
)+…+
×(
-
)
=
×(1-
)
=
×
=
.
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 3 |
| 1 |
| 3 |
| 1 |
| 4 |
| 1 |
| 7 |
| 1 |
| 8 |
=1-
| 1 |
| 8 |
=
| 7 |
| 8 |
(2)原式=
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 4 |
| 1 |
| 5 |
| 1 |
| 9 |
| 1 |
| 4 |
| 1 |
| 9 |
| 1 |
| 13 |
| 1 |
| 4 |
| 1 |
| 2005 |
| 1 |
| 2009 |
=
| 1 |
| 4 |
| 1 |
| 2009 |
=
| 1 |
| 4 |
| 2008 |
| 2009 |
=
| 502 |
| 2009 |
点评:此题考查有理数的混合运算,掌握运算顺序,正确根据数的特点选择适当的方法简算.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目
一家商店一月份把某种进货价为100元的商品,提高60%出售,到三月份再声称以8折(80%)大拍卖,那么该商品三月份的价格比进货价( )
| A、高12.8%元 |
| B、低12.8%元 |
| C、高40元 |
| D、高28元 |
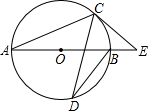 如图所示,线段AB是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,求∠E的度数.
如图所示,线段AB是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,求∠E的度数.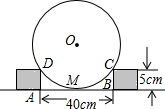 如图,为了测量圆形工件的直径,在工作台上用边长都为5cm的两个立方体小木块顶在圆形工件的两侧,测得两木块间的距离AB=40cm.
如图,为了测量圆形工件的直径,在工作台上用边长都为5cm的两个立方体小木块顶在圆形工件的两侧,测得两木块间的距离AB=40cm. 如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是60,AB=18,BC=12,则DE=
如图,BD是∠ABC的角平分线,DE⊥AB于E,△ABC的面积是60,AB=18,BC=12,则DE=