题目内容
 如图,在Rt△ABC中,∠B=90°,AD=AB=BC,DE⊥AC.求证:BE=DC.
如图,在Rt△ABC中,∠B=90°,AD=AB=BC,DE⊥AC.求证:BE=DC.考点:全等三角形的判定与性质,等腰直角三角形
专题:
分析:连接AE,先证得RT△ABE≌RT△ADE得出BE=DE,然后证得△EDC是等腰直角三角形,得出DE=DC,即可证得BE=DC.
解答:证明:连接AE,
∵DE⊥AC.
∴∠ADE=90°,
在RT△ABE和RT△ADE中,
,
∴RT△ABE≌RT△ADE(HL),
∴BE=DE,
∵∠B=90°,AB=BC,
∴△ABC是等腰直角三角形,
∴∠C=45°,
∵DE⊥AC.
∴△EDC是等腰直角三角形,
∴DE=DC,
∴BE=DC.
∵DE⊥AC.
∴∠ADE=90°,
在RT△ABE和RT△ADE中,
|
∴RT△ABE≌RT△ADE(HL),
∴BE=DE,
∵∠B=90°,AB=BC,
∴△ABC是等腰直角三角形,
∴∠C=45°,
∵DE⊥AC.
∴△EDC是等腰直角三角形,
∴DE=DC,
∴BE=DC.
点评:本题考查了全等三角形判定和性质,等腰直角三角形的判定和性质,证得BE=DE,DE=DC是本题的关键.

练习册系列答案
 桃李文化快乐暑假武汉出版社系列答案
桃李文化快乐暑假武汉出版社系列答案 优秀生快乐假期每一天全新寒假作业本系列答案
优秀生快乐假期每一天全新寒假作业本系列答案 暑假接力赛新疆青少年出版社系列答案
暑假接力赛新疆青少年出版社系列答案
相关题目
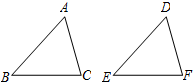 如图,给出下列四组条件,其中,不能使△ABC≌△DEF的条件是( )
如图,给出下列四组条件,其中,不能使△ABC≌△DEF的条件是( )| A、AB=DE,BC=EF,AC=DF |
| B、AB=DE,∠B=∠E,BC=EF |
| C、∠B=∠E,BC=EF,∠C=∠F |
| D、AB=DE,AC=DF,∠B=∠E |
 如下图,一个点从数轴上的原点开始,先向右移动了3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.已知点A、B是数轴上的点,完成下列各题:
如下图,一个点从数轴上的原点开始,先向右移动了3个单位长度,再向左移动5个单位长度,可以看到终点表示的数是-2.已知点A、B是数轴上的点,完成下列各题: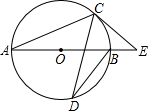 如图所示,线段AB是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,求∠E的度数.
如图所示,线段AB是⊙O上一点,∠CDB=20°,过点C作⊙O的切线交AB的延长线于点E,求∠E的度数.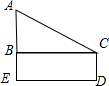 Rt△ABC中,∠ABC=90°,∠ACB=30°,四边形BCDE为矩形,且CD=
Rt△ABC中,∠ABC=90°,∠ACB=30°,四边形BCDE为矩形,且CD= 作图题(保留作图痕迹,不写作法).
作图题(保留作图痕迹,不写作法). 如图,以矩形ABDE的一边BD为直径作半圆O,BE交圆O于C,AC的延长线交ED于M,交BD的延长线于N,若ME=MC.
如图,以矩形ABDE的一边BD为直径作半圆O,BE交圆O于C,AC的延长线交ED于M,交BD的延长线于N,若ME=MC.