题目内容
4.在平面直角坐标系中,已知点A(-2,4),B(-3,1),以原点O为位似中心,相似比为2,把△ABO放大,则点A的对应点A′的坐标是( )| A. | (-4,8) | B. | (-1,2) | C. | (-4,8)或(4,-8) | D. | (-1,2)或(1,-2) |
分析 直接根据如果位似变换是以原点为位似中心,相似比为k,那么位似图形对应点的坐标的比等于k或-k进行解答.
解答 解:∵以原点O为位似中心,相似比为2,将△OAB放大为△OA′B′,点A(-2,4),
∴A′点的坐标为(-4,8),B′(4,-8).
故选:C.
点评 此题主要考查了位似变换的性质,根据各点到位似中心的距离比也等于相似比是解决问题的关键.

练习册系列答案
 励耘书业暑假衔接宁波出版社系列答案
励耘书业暑假衔接宁波出版社系列答案
相关题目
15.-3的负倒数( )
| A. | 3 | B. | -3 | C. | $\frac{1}{3}$ | D. | -$\frac{1}{3}$ |
12.不等式4x-8≤0的解集是( )
| A. | x≥-2 | B. | ≤-2 | C. | ≥2 | D. | ≤2 |
19. 已知?ABCD的对角线AC与BD交于点O,下列结论不正确的是( )
已知?ABCD的对角线AC与BD交于点O,下列结论不正确的是( )
 已知?ABCD的对角线AC与BD交于点O,下列结论不正确的是( )
已知?ABCD的对角线AC与BD交于点O,下列结论不正确的是( )| A. | 当AB=BC时,?ABCD是菱形 | B. | 当AC⊥BD时,?ABCD是菱形 | ||
| C. | 当OA=OB时,?ABCD是矩形 | D. | 当∠ABD=∠CBD时,?ABCD是矩形 |
9.2${\;}^{-\frac{1}{2}}$等于( )
| A. | $\sqrt{2}$ | B. | -$\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | -$\frac{\sqrt{2}}{2}$ |
13.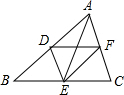 如图,D、E、F分别是△ABC各边的中点.添加下列条件后,不能得到四边形ADEF是矩形的是( )
如图,D、E、F分别是△ABC各边的中点.添加下列条件后,不能得到四边形ADEF是矩形的是( )
 如图,D、E、F分别是△ABC各边的中点.添加下列条件后,不能得到四边形ADEF是矩形的是( )
如图,D、E、F分别是△ABC各边的中点.添加下列条件后,不能得到四边形ADEF是矩形的是( )| A. | ∠BAC=90° | B. | BC=2AE | C. | DE平分∠AEB | D. | AE⊥BC |
14.下列计算正确的是( )
| A. | (x+y)2=x2+y2 | B. | (x-y)2=x2-2xy-y2 | C. | x(x-1)=x2-1 | D. | (x+1)(x-1)=x2-1 |
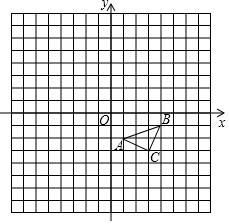 如图.在平面直角坐标系内,△ABC三个顶点的坐标分别为A(1,-2),B(4,-1),C(3,-3)(正方形网格中,每个小正方形的边长都是1个单位长度).
如图.在平面直角坐标系内,△ABC三个顶点的坐标分别为A(1,-2),B(4,-1),C(3,-3)(正方形网格中,每个小正方形的边长都是1个单位长度).