题目内容
已知AD、BE是△ABC的两条中线，且△ADE的面积是4，则△ABC的面积是（ ）
| A、8 | B、12 | C、16 | D、20 |
考点：三角形的面积
专题：
分析：先根据AD是△ABC的中线可知S△ADC=
S△ABC，再由DE是△ADC的中线可知S△ADE=
S△ADC，故可得出结论．
| 1 |
| 2 |
| 1 |
| 2 |
解答：
解：∵AD是△ABC的中线，
∴S△ADC=
S△ABC．
∵△ABC的是中线，
∴BE是DE是△ADC的中线，
∴S△ADE=
S△ADC，
∴S△ABC=4S△ADC=4×4=16．
故选C．
解：∵AD是△ABC的中线，∴S△ADC=
| 1 |
| 2 |
∵△ABC的是中线，
∴BE是DE是△ADC的中线，
∴S△ADE=
| 1 |
| 2 |
∴S△ABC=4S△ADC=4×4=16．
故选C．
点评：本题考查的是三角形的面积，熟知三角形的中线将三角形的面积分为相等的两部分是解答此题的关键．
练习册系列答案
相关题目
已知．B在A的北偏东30°，则A在B的（ ）
| A、南偏东30° |
| B、南偏东60° |
| C、南偏西30° |
| D、北偏西60° |
下列运算正确的是（ ）
| A、（-2a3）2=4a5 | ||||
| B、（a-b）2=a2-b2 | ||||
C、
| ||||
D、-
|
如图，在矩形ABCD中，E是BC边上的点，且CE=2BE，△DEF的面积等于2，则此矩形的面积等于
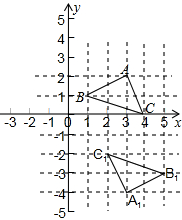如图，在平面直角坐标系中，若△BAC与△A1B1C1关于点E成中心对称，则对称中心点E的坐标是（ ）| A、（2，-1） |
| B、（3，-1） |
| C、（4，-1） |
| D、（3，-2） |