题目内容
6.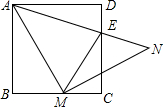 如图,在正方形ABCD中,M是BC边上一点,连AM,作MN⊥AM,且MN=AM,连接AN交BC于E,连接ME.
如图,在正方形ABCD中,M是BC边上一点,连AM,作MN⊥AM,且MN=AM,连接AN交BC于E,连接ME.(1)求证:MN平分∠CME;
(2)若AB=4,CE=3,求CM的长.
分析 (1)将△ADE绕点A顺时针旋转90°得到△ABH,作AK⊥ME,先证明△AMH≌△AME得AB=AK(全等三角形对应边上的高相等),所以∠AMB=∠AMK,再利用等角的余角相等证明MN平分∠CME即可.
(2)先证明:EM=BM+DE,在RT△EMC中利用勾股定理解决即可.
解答 解: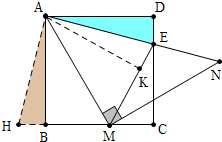 如图所示,将△ADE绕点A顺时针旋转90°得到△ABH,作AK⊥ME,
如图所示,将△ADE绕点A顺时针旋转90°得到△ABH,作AK⊥ME,
∵MA=MN,∠AMN=90°,
∴∠MAN=∠MNA=45°,
∵四边形ABCD是正方形,
∴AB=AD,∠DAB=90°,
∴∠MAB+∠DAE=45°,
∵∠DAE=∠HAB,
∴∠HAB+∠BAM=45°=∠MAE,
在△AMH和△AME中,
$\left\{\begin{array}{l}{AM=AM}\\{∠MAH=∠MAE}\\{AH=AE}\end{array}\right.$,
∴△AMH≌△AME,
∴ME=MH=BM+BH=BM+DE,AB=AK(全等三角形对应边上的高相等),
∵AB⊥BM,AK⊥EM
∴∠AMB=∠AMK,
∵∠AMB+∠NMC=90°,∠AMK+∠EMN=90°,
∴∠EMN=∠NMC,
∴MN平分∠CME.
(2)由(1)可知:ME=BM+DE,设CM=x,则BM=4-x,ME=1+(4-x)=5-x,
在RT△EMC中,∵EM2=EC2+MC2,
∴(5-x)2=x2+32,
∴x=$\frac{8}{5}$,
∴CM=$\frac{8}{5}$.
点评 本题考查正方形的性质、勾股定理、全等三角形的判定和性质等知识,解题关键是利用旋转添加辅助线,构造全等三角形,属于中考常考题型.

练习册系列答案
 暑假衔接教材期末暑假预习武汉出版社系列答案
暑假衔接教材期末暑假预习武汉出版社系列答案 假期作业暑假成长乐园新疆青少年出版社系列答案
假期作业暑假成长乐园新疆青少年出版社系列答案
相关题目
15.方程组$\left\{\begin{array}{l}{x+y=3}\\{x-y=1}\end{array}\right.$的解为( )
| A. | $\left\{\begin{array}{l}{x=3}\\{y=0}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x=3}\\{y=2}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x=2}\\{y=1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{x=-1}\\{y=-2}\end{array}\right.$ |
 如图,在数轴上,点A和点B表示的数分别为-$\sqrt{2}$,$\sqrt{7}$,则点A和点B之间表示正整数的点有4个.
如图,在数轴上,点A和点B表示的数分别为-$\sqrt{2}$,$\sqrt{7}$,则点A和点B之间表示正整数的点有4个.
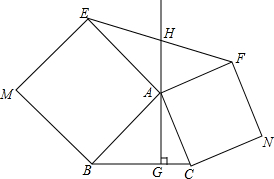 同学们小学学习了正方形,正方形就是四条边都相等,四个角都是直角.如图,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作正方形ABME和正方形ACNF,射线GA交EF于点H,试探究HE与HF之间的数量关系,并说明理由.
同学们小学学习了正方形,正方形就是四条边都相等,四个角都是直角.如图,△ABC中,AG⊥BC于点G,分别以AB、AC为一边向△ABC外作正方形ABME和正方形ACNF,射线GA交EF于点H,试探究HE与HF之间的数量关系,并说明理由. 如图,△ABC中,AB=BC,∠ABC=120°,E是线段AC上一点,AE=3EC,连接BE并延长至D,连接CD,若∠BCD=120°,AB=6,则线段CD长为3.
如图,△ABC中,AB=BC,∠ABC=120°,E是线段AC上一点,AE=3EC,连接BE并延长至D,连接CD,若∠BCD=120°,AB=6,则线段CD长为3. 已知二次函数y=x2-4x.
已知二次函数y=x2-4x.