题目内容
19.若x:y=1:3,则$\frac{2x+y}{x-y}$的值是-$\frac{5}{2}$.分析 根据比例的性质,可用x表示y,根据分式的性质,可得答案.
解答 解:由比例的性质,得
y=3x.
$\frac{2x+y}{x-y}$=$\frac{2x+3x}{x-3x}$=-$\frac{5}{2}$,
故答案为:-$\frac{5}{2}$.
点评 本题考查了比例的性质,利用比例的性质的出y=3x是解题关键.

练习册系列答案
相关题目
2.某工厂计划在规定日期内生产某种产品200个,按计划生产2天后,由于改进工艺,每天产量比原计划多生产5个,因此提前6天完成任务.求计划每天生产这种产品多少个?
在解题时,设原计划每天生产x个,则下列方程正确的是( )
在解题时,设原计划每天生产x个,则下列方程正确的是( )
| A. | $\frac{200}{x+5}$=$\frac{200}{x}$-6 | B. | $\frac{200-2x}{x+5}$=$\frac{200}{x}$-6 | ||
| C. | $\frac{200-2x}{x+5}=\frac{200}{x}$+6 | D. | $\frac{200-2x}{x}$-$\frac{200-2x}{x+5}$=6. |
7.某学校会议室的面积为64m2,会议室地面恰由100块相同的正方形地砖铺成,每块地砖的边长是( )
| A. | 0.64m | B. | 0.8m | C. | 8m | D. | 10m |
14.数值在2和3之间的数是( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | $\sqrt{5}$ | D. | $\sqrt{10}$ |
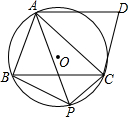 已知:如图,在平行四边形ABCD中,⊙O是经过A、B、C三点的圆,CD与⊙O相切于点C,点P是$\widehat{BC}$上的一个动点(点P不与B、C点重合),连接PA、PB、PC.
已知:如图,在平行四边形ABCD中,⊙O是经过A、B、C三点的圆,CD与⊙O相切于点C,点P是$\widehat{BC}$上的一个动点(点P不与B、C点重合),连接PA、PB、PC. 如图,已知OM平分∠AOC,ON平分∠BOC,∠AOB=90°,∠BOC=30°.
如图,已知OM平分∠AOC,ON平分∠BOC,∠AOB=90°,∠BOC=30°.