Question

1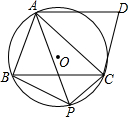．已知：如图，在平行四边形ABCD中，⊙O是经过A、B、C三点的圆，CD与⊙O相切于点C，点P是$\widehat{BC}$上的一个动点（点P不与B、C点重合），连接PA、PB、PC．
（1）求证：CA=CB；
（2）①点P满足当AC=AP时，△CPA≌△ABC，请说明理由；
②当∠ABC的度数为60时，四边形ABCD是菱形．

Answer 1

分析 （1）作CE⊥AB于E，由于CA=CB，根据等腰三角形的性质得CE为AB的垂直平分线，则点O在CE上，再根据平行四边形的性质得AB∥CD，
（2）当AC=AP时，△CPA≌△ABC．由于AC=BC，AC=AP，则∠ABC=∠BAC，∠APC=∠ACP，根据圆周角定理得∠ABC=∠APC，则∠BAC=∠ACP，加上AC=CA，即可得到△CPA≌△ABC；
（3）如图2，连接OC，AC，OB，根据平行线的性质得到∠BCD=120°，根据切线的性质得到∠OCD=90°，推出BO垂直平分AC，即可得到结论．

解答 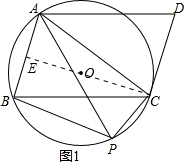（1）证明：
连接CO并延长交AB于E，如图，
∵CD与⊙O相切于点C，
∴CE⊥CD，
∵四边形ABCD为平行四边形，
∴AB∥CD，
∴CE⊥AB，
∴AE=BE，
∴BC=AC；

（2）解：当AC=AP时，△CPA≌△ABC．
证明如下：∵AC=BC，AC=AP，
∴∠ABC=∠BAC，∠APC=∠ACP，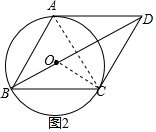
∵∠ABC=∠APC，
∴∠BAC=∠ACP，
在△CPA与△ABC中，$\left\{\begin{array}{l}{∠APC=∠ABC}\\{∠ACP=∠CAB}\\{AC=CA}\end{array}\right.$，
∴△CPA≌△ABC；
故答案为：AC=AP；

（3）解：当∠ABC的度数为60°时，四边形ABCD是菱形，
如图2，连接OC，AC，OB，
∵∠ABC=60°，
∴∠BCD=120°，
∵CD与⊙O相切于点C，
∴∠OCD=90°，
∴∠BCO=30°，
∵OB=OC，
∴∠OBC=30°，
∴∠ABO=30°，
∴BO垂直平分AC，
∴AB=BC，
∴四边形ABCD是菱形．
故答案为：60°．

点评 本题考查了切线的性质，经过半径的外端且垂直于这条半径的直线是圆的切线．也考查了全等三角形的判定与性质和平行四边形的性质．