题目内容
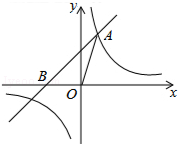 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=| k |
| x |
(1)求两个函数的解析式;
(2)求△OAB的面积.
考点:反比例函数与一次函数的交点问题
专题:
分析:(1)根据待定系数法,把A(2,5)分别代入y=
和y=x+b,可得k与b的值.从而得出答案;
(2)作AC⊥x轴于点C,根据三角形的面积公式,即可得出答案.
| k |
| x |
(2)作AC⊥x轴于点C,根据三角形的面积公式,即可得出答案.
解答: 解:(1)把A(2,5)分别代入y=
解:(1)把A(2,5)分别代入y=
和y=x+b,得
,
解得k=10,b=3;
(2)作AC⊥x轴于点C,
由(1)得直线AB的解析式为y=x+3,
∴点B的坐标为(-3,0),
∴OB=3,
∵点A的坐标是(2,5),
∴AC=5,
∴S△OAB=
OB•AC=
×3×5=
.
 解:(1)把A(2,5)分别代入y=
解:(1)把A(2,5)分别代入y=| k |
| x |
|
解得k=10,b=3;
(2)作AC⊥x轴于点C,
由(1)得直线AB的解析式为y=x+3,
∴点B的坐标为(-3,0),
∴OB=3,
∵点A的坐标是(2,5),
∴AC=5,
∴S△OAB=
| 1 |
| 2 |
| 1 |
| 2 |
| 15 |
| 2 |
点评:本题考查了反比例函数与一次函数的交点问题,利用了待定系数法,三角形的面积公式.

练习册系列答案
相关题目
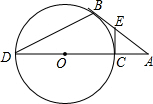 如图,AB是⊙O的切线,切点为B,直线AO交⊙O于点C、D,若∠A=30°.
如图,AB是⊙O的切线,切点为B,直线AO交⊙O于点C、D,若∠A=30°.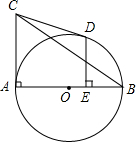 如图,已知AB为⊙O的直径,AC切⊙O于点A,过C作⊙O的切线CD,切⊙O于D.DE⊥AB于点E,连接BC交于点F.求证:DF=FE.
如图,已知AB为⊙O的直径,AC切⊙O于点A,过C作⊙O的切线CD,切⊙O于D.DE⊥AB于点E,连接BC交于点F.求证:DF=FE. 游艇在湖面上以12千米/小时的速度向正东方向航行,在O处看到灯塔A在游艇北偏东60°方向上,航行1小时到达B处,此时看到灯塔A在游艇北偏西30°方向上,求此时游艇与灯塔的距离AB.
游艇在湖面上以12千米/小时的速度向正东方向航行,在O处看到灯塔A在游艇北偏东60°方向上,航行1小时到达B处,此时看到灯塔A在游艇北偏西30°方向上,求此时游艇与灯塔的距离AB.