题目内容
 游艇在湖面上以12千米/小时的速度向正东方向航行,在O处看到灯塔A在游艇北偏东60°方向上,航行1小时到达B处,此时看到灯塔A在游艇北偏西30°方向上,求此时游艇与灯塔的距离AB.
游艇在湖面上以12千米/小时的速度向正东方向航行,在O处看到灯塔A在游艇北偏东60°方向上,航行1小时到达B处,此时看到灯塔A在游艇北偏西30°方向上,求此时游艇与灯塔的距离AB.考点:解直角三角形的应用-方向角问题
专题:
分析:将实际问题转化为数学问题,并构造出与实际问题有关的直角三角形,过点A作AC⊥OB交OB于C,则AC为所求的最短距离,即可得出答案.
解答: 解:过点A作AC⊥OB交OB于C,则AC为所求,设AC=x,
解:过点A作AC⊥OB交OB于C,则AC为所求,设AC=x,
由题意得:OB=12千米,∠AOC=30°,∠ABC=60°,
在Rt△ACO和Rt△ACB中:
tan30°=
,tan60°=
,
则OC=
x,BC=
x,
而OC+CB=
x+
x=12,
解得:x=3
.
答:灯塔A到航线OB的最短距离为3
千米.
 解:过点A作AC⊥OB交OB于C,则AC为所求,设AC=x,
解:过点A作AC⊥OB交OB于C,则AC为所求,设AC=x,由题意得:OB=12千米,∠AOC=30°,∠ABC=60°,
在Rt△ACO和Rt△ACB中:
tan30°=
| x |
| OC |
| x |
| BC |
则OC=
| 3 |
| ||
| 3 |
而OC+CB=
| 3 |
| ||
| 3 |
解得:x=3
| 3 |
答:灯塔A到航线OB的最短距离为3
| 3 |
点评:此题主要考查了解直角三角形的应用,通过作辅助线构造直角三角形,再把条件和问题转化到这个直角三角形中,使问题得以解决.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
一个长方形的一边长是2a+3b,另一边的长是a-b,则这个长方形的周长是( )
| A、6a+3b |
| B、3a-2b |
| C、3a+3b |
| D、6a+4b |
下列各组单项式中,不是同类项的是( )
A、12y与
| ||||
| B、6mb与-bm | ||||
| C、23与32 | ||||
D、
|
若一元二次方程ax2+bx+c=0无解,且a<0,则二次函数y=ax2+bx+c的值( )
| A、总大于0 | ||
| B、总小于0 | ||
C、在x>-
| ||
D、在x>-
|
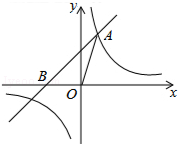 如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=
如图,已知在平面直角坐标系xOy中,O是坐标原点,点A(2,5)在反比例函数y=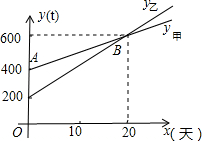 如图,AB、CB表示某工厂甲、乙两车间的产量y(t)与所用时间x(天)之间的函数图象,根据图象回答下列问题:
如图,AB、CB表示某工厂甲、乙两车间的产量y(t)与所用时间x(天)之间的函数图象,根据图象回答下列问题: 如图,已知△XYZ中,MY=NZ,A、B分别是YN、MZ的中点,延长AB、BA分别交XZ、XY于点D、C,求证:XC=XD.
如图,已知△XYZ中,MY=NZ,A、B分别是YN、MZ的中点,延长AB、BA分别交XZ、XY于点D、C,求证:XC=XD.