题目内容
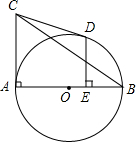如图，已知AB为⊙O的直径，AC切⊙O于点A，过C作⊙O的切线CD，切⊙O于D．DE⊥AB于点E，连接BC交于点F．求证：DF=FE．考点：切线的性质
专题：证明题
分析：如图，作辅助线；证明CA=CD（设为λ），BG=DG（设为μ），AC∥DE∥BG，得到△CDF∽△CGB；列出比例式求得DF=
；同理可求得EF=
，问题即可解决．
| λμ |
| λ+μ |
| λμ |
| λ+μ |
解答：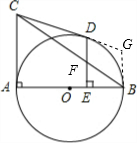
解：如图，过点B作⊙O的切线BG，交AD的延长线于点G；
∵AC、CD、BG分别为⊙O的切线，
∴CA=CD（设为λ），BG=DG（设为μ），
AC⊥AB，BG⊥AB；而DE⊥AB，
∴AC∥DE∥BG，
∴△CDF∽△CGB，
∴
=
，DF=
；
∵△BEF∽△BAC，
∴
=
，而
=
=
，
∴EF=
，
∴DF=EF．
解：如图，过点B作⊙O的切线BG，交AD的延长线于点G；∵AC、CD、BG分别为⊙O的切线，
∴CA=CD（设为λ），BG=DG（设为μ），
AC⊥AB，BG⊥AB；而DE⊥AB，
∴AC∥DE∥BG，
∴△CDF∽△CGB，
∴
| DF |
| μ |
| λ |
| λ+μ |
| λμ |
| λ+μ |
∵△BEF∽△BAC，
∴
| EF |
| λ |
| BE |
| BA |
| BE |
| BA |
| DG |
| CG |
| μ |
| λ+μ |
∴EF=
| λμ |
| λ+μ |
∴DF=EF．
点评：该题主要考查了切线的性质及其应用问题；解题的关键是作辅助线，灵活运用切线的性质定理等几何知识点来分析、判断、推理或解答．
练习册系列答案
浙江名校名师金卷系列答案
相关题目
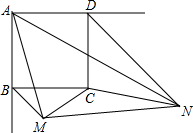已知：如图，正方形ABCD的边长为6，BM，DN分别平分正方形的两个外角，且满足∠MAN=45°，连接MC，NC，MN．
如图，△ABD和△CBD都是等边三角形，点E从A出发向D运动（但不与点A、D重合），同时点F以相同的速度从D出发向C运动（但不与点D、C重合）．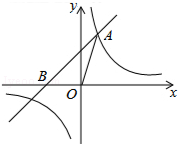
如图，已知在平面直角坐标系xOy中，O是坐标原点，点A（2，5）在反比例函数y=
问题：如图1，在Rt△ABC中，∠C=90°，⊙O是Rt△ABC的内切圆，切点分别是D、E、F，若三角形三边长分别记为BC=a，AC=b，AB=c，内切圆半径记为r，现有小尧和小淇对半径进行计算．下面是两位同学简要的解答过程：