题目内容
18.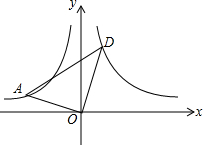 如图,∠AOB=90°,且点A,B分别在反比例函数y=$\frac{{k}_{1}}{x}$(x<0),y=$\frac{{k}_{2}}{x}$(x>0)的图象上,且k1,k2分别是方程x2-x-6=0的两根.
如图,∠AOB=90°,且点A,B分别在反比例函数y=$\frac{{k}_{1}}{x}$(x<0),y=$\frac{{k}_{2}}{x}$(x>0)的图象上,且k1,k2分别是方程x2-x-6=0的两根.(1)求k1,k2的值;
(2)连接AB,求tan∠OBA的值.
分析 (1)解方程x2-x-6=0求出方程两根,即可得到k1,k2的值;
(2)过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.易证△ACO∽△ODB,由相似三角形的性质可求出OA:OB的值,进而可求出tan∠OBA的值.
解答 解:(1)∵k1,k2分别是方程x2-x-6=0的两根,
∴解方程x2-x-6=0,得x1=3,x2=-2.结合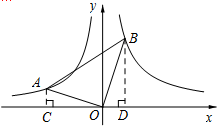 图象可知:k1<0,k2>0,
图象可知:k1<0,k2>0,
∴k1=-2,k2=3.
(2)如图,过点A作AC⊥x轴于点C,过点B作BD⊥y轴于点D.
由(1)知,点A,B分别在反比例函数y=-$\frac{2}{x}$(x<0),y=$\frac{3}{x}$(x>0)的图象上,
∴S△ACO=$\frac{1}{2}$×|-2|=1,S△ODB=$\frac{1}{2}$×3=1.5.
∵∠AOB=90°,
∴∠AOC+∠BOD=90°,
∵∠AOC+∠OAC=90°,
∴∠OAC=∠BOD.
又∵∠ACO=∠ODB=90°,
∴△ACO∽△ODB.
∴$\frac{{S}_{△ACO}}{{S}_{△OBD}}$=$\frac{2}{3}$,
∴$\frac{OA}{OB}$=±$\frac{\sqrt{6}}{3}$(舍负取正),
即$\frac{OA}{OB}=\frac{\sqrt{6}}{3}$.
∴在Rt△AOB中,tan∠OBA=$\frac{OA}{OB}$=$\frac{\sqrt{6}}{3}$.
点评 本题主要考查了相似三角形的判定与性质及反比例函数图象上点的坐标特征,解题的关键是正确作出辅助线,构造相似三角形.

练习册系列答案
相关题目
20.物理实验过程:如图甲所示,以初始速度v0(m/s)用小锤击打弱性金属片,不考虑空气阻力时,小球做平抛运动.用频闪照相的方法观测到小球在下落过程中的几个位置(图乙),用平滑曲线把这些位置连起来,就得到平抛运动的轨迹(图丙).
数学问题:在图丙中,以小球被击出的水平方向为x轴正方向,竖直向下的方向为y轴正方向,小球被击出点为原点建立直角坐标系,得到小球的位置坐标(x,y)(x>0,y>0).由物理知识可得到x(m),y(m)与时间t(s)的关系如下:①x=v0t;②y=$\frac{1}{2}$gt2.
由实验测得3个时刻小球的位置坐标如下表所示.
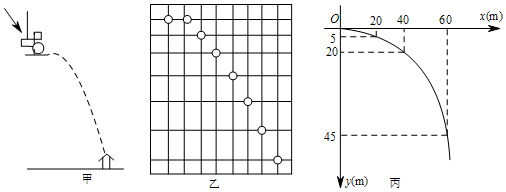
(1)v0=20m/s,g=10m/s2.
(2)求出y与x之间的函数关系式.
(3)当小球在竖直方向上下落80m时,它在水平方向上前进了多少?
数学问题:在图丙中,以小球被击出的水平方向为x轴正方向,竖直向下的方向为y轴正方向,小球被击出点为原点建立直角坐标系,得到小球的位置坐标(x,y)(x>0,y>0).由物理知识可得到x(m),y(m)与时间t(s)的关系如下:①x=v0t;②y=$\frac{1}{2}$gt2.
由实验测得3个时刻小球的位置坐标如下表所示.
| t(s) | 1 | 2 | 3 |
| x(m) | 20 | 40 | 60 |
| y(m) | 5 | 20 | 45 |

(1)v0=20m/s,g=10m/s2.
(2)求出y与x之间的函数关系式.
(3)当小球在竖直方向上下落80m时,它在水平方向上前进了多少?

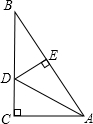 在Rt△ABC中,如图所示,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE=3.8cm,则BC等于11.4cm.
在Rt△ABC中,如图所示,∠C=90°,∠CAB=60°,AD平分∠CAB,点D到AB的距离DE=3.8cm,则BC等于11.4cm.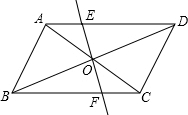 如图,已知O是?ABCD的对角线的交点,过点O作直线分别与AD和BC相交于点E、F,求证:OE=OF.
如图,已知O是?ABCD的对角线的交点,过点O作直线分别与AD和BC相交于点E、F,求证:OE=OF.
 [问题提出]
[问题提出]