题目内容
9.已知x=$\sqrt{2}-1$,y=$\sqrt{2}+1$,求$\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}-{y}^{2}}$的值.分析 首先将分式因式分解进而将已知代入求出即可.
解答 解:∵x=$\sqrt{2}-1$,y=$\sqrt{2}+1$,
∴$\frac{{x}^{2}-2xy+{y}^{2}}{{x}^{2}-{y}^{2}}$
=$\frac{(x-y)^{2}}{(x+y)(x-y)}$
=$\frac{x-y}{x+y}$
=$\frac{\sqrt{2}-1-\sqrt{2}-1}{\sqrt{2}-1+\sqrt{2}+1}$
=$\frac{-2}{2\sqrt{2}}$
=-$\frac{\sqrt{2}}{2}$.
点评 此题主要考查了二次根式的化简求值,正确分解因式得出是解题关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20. 如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )
 如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )
如图,四边形ABCD是⊙O的内接四边形,若∠BOD=88°,则∠BCD的度数是( )| A. | 88° | B. | 92° | C. | 106° | D. | 136° |
3.正方形具有而菱形不一定具有的特征有( )
| A. | 对角线互相垂直平分 | B. | 内角和为360° | ||
| C. | 对角线相等 | D. | 对角线平分内角 |
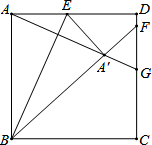 如图,点E为正方形ABCD边AD上的一点,且AE:DE=4:5,连接BE,将正方形沿着BE折叠,使A点落在A′点处,分别连接BA′、AA′交CD于点F、G.若FG=1,则正方形ABCD的边长为$\frac{72}{25}$.
如图,点E为正方形ABCD边AD上的一点,且AE:DE=4:5,连接BE,将正方形沿着BE折叠,使A点落在A′点处,分别连接BA′、AA′交CD于点F、G.若FG=1,则正方形ABCD的边长为$\frac{72}{25}$.