题目内容
11. 如图,在△ABC中,∠ACB=90°,△CAD≌△CED,△CEF≌△BEF,△CEF≌△CAD.
如图,在△ABC中,∠ACB=90°,△CAD≌△CED,△CEF≌△BEF,△CEF≌△CAD.(1)求∠A,∠B的度数;
(2)猜想AC,EF的位置关系,并说明理由.
分析 (1)由△CAD≌△CED,△CEF≌△CAD,根据全等三角形的对应角相等可得∠ADC=∠ACD=∠ECD,∠ECF=∠ACD,则∠ACB=3∠ECF=90°,∠ECF=30°,再由△CEF≌△BEF,得出∠ECF=∠B=30°,然后根据直角三角形两锐角互余求出∠A=60°;
(2)由△CEF≌△BEF,得出∠CFE=∠BFE,又∠CFE+∠BFE=180°,求出∠CFE=90°,在直角△CEF中,根据30°角所对的直角边等于斜边的一半得出EF=$\frac{1}{2}$CE,又由△CAD≌△CED,得出AC=CE,等量代换得到EF=$\frac{1}{2}$AC.
解答 解:(1)∵△CAD≌△CED,△CEF≌△CAD,
∴∠ADC=∠ACD=∠ECD,∠ECF=∠ACD,
∴∠ACB=∠ACD+∠ECD+∠ECF=3∠ECF=90°,
解得∠ECF=30°,
∵△CEF≌△BEF,
∴∠ECF=∠B=30°,
∴∠A=90°-∠B=60°;
(2)EF=$\frac{1}{2}$AC,理由如下:
∵△CEF≌△BEF,
∴∠CFE=∠BFE,
∵∠CFE+∠BFE=180°,
∴∠CFE=90°.
∵在直角△CEF中,∠CFE=90°,∠ECF=30°,
∴EF=$\frac{1}{2}$CE,
又△CAD≌△CED,
∴AC=CE,
∴EF=$\frac{1}{2}$AC.
点评 本题考查了全等三角形的对应边相等,全等三角形的对应角相等的性质,直角三角形两锐角互余的性质,30°角所对的直角边等于斜边的一半的性质,求出∠B=30°是解题的关键.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
1.下列说法不正确的是( )
| A. | 平行四边形的对角互补,邻角相等 | |
| B. | 平行四边形的对角线互相平分 | |
| C. | 有两组对边分别平行的四边形是平行四边形 | |
| D. | 平行四边形的对边平行且相等 |

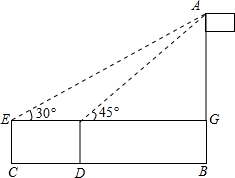 如图,身高1.6米的小明为了测量学校旗杆AB的高度,在平地上C处测得旗杆高度顶端A的仰角为30°,沿CB方向前进3米到达D处,在D处测得旗杆顶端A的仰角为45°,求旗杆AB的高度($\sqrt{3}=1.7,\sqrt{2}=1.4$)
如图,身高1.6米的小明为了测量学校旗杆AB的高度,在平地上C处测得旗杆高度顶端A的仰角为30°,沿CB方向前进3米到达D处,在D处测得旗杆顶端A的仰角为45°,求旗杆AB的高度($\sqrt{3}=1.7,\sqrt{2}=1.4$)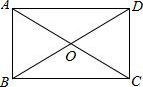 如图,在矩形ABCD中,AB比AD的一半长2cm,AD=10cm,问△ABD的周长比△AOD的周长长多少?
如图,在矩形ABCD中,AB比AD的一半长2cm,AD=10cm,问△ABD的周长比△AOD的周长长多少? 如图是一块正三角形花圃,为了分别种上红、黄、紫三种颜色的花,要求把它划分成三块面积相同的部分,并且使整个图形呈轴对称图形,请你至少设计三种不同方案.
如图是一块正三角形花圃,为了分别种上红、黄、紫三种颜色的花,要求把它划分成三块面积相同的部分,并且使整个图形呈轴对称图形,请你至少设计三种不同方案.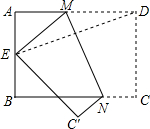 如图,四边形ABCD为矩形,AB=6,BC=8,E为AB的中点,将矩形ABCD折叠,使得点D与点E重合,折痕为MN,则折痕MN的长度为$\frac{3\sqrt{73}}{4}$.
如图,四边形ABCD为矩形,AB=6,BC=8,E为AB的中点,将矩形ABCD折叠,使得点D与点E重合,折痕为MN,则折痕MN的长度为$\frac{3\sqrt{73}}{4}$.