Question

18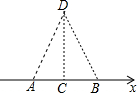．如图，长为12cm的弹性皮筋直放置在x轴上，固定两端A和B，然后把中点C向上拉升8cm至D点，则弹性皮筋被拉长了8cm．

Answer 1

分析 根据勾股定理，可求出AD、BD的长，则AD+BD-AB即为橡皮筋拉长的距离．

解答 解：根据题意得：AD=BD，AC=BC，AB⊥CD，
则在Rt△ACD中，AC=$\frac{1}{2}$AB=6cm，CD=8cm；
根据勾股定理，得：AD=$\sqrt{A{C}^{2}+C{D}^{2}}$=$\sqrt{{6}^{2}+{8}^{2}}$=10（cm）；
所以AD+BD-AB=2AD-AB=20-12=8（cm）；
即橡皮筋被拉长了8cm；
故答案为：8cm．

点评 此题主要考查了等腰三角形的性质以及勾股定理的应用；熟练掌握等腰三角形的性质，由勾股定理求出AD是解决问题的关键．